2 FastText架构介绍¶

学习目标¶

了解FastText的模型架构
了解FastText模型中层次化的softmax
了解负采样

2.1 FastText模型架构¶

FastText在词向量训练上使用了与Word2Vec类似的模型架构，但有所改进。FastText可以基于两种训练方式：

Skip-gram模型
- 在Skip-gram模型中，给定一个中心词（目标词），模型的目标是通过预测上下文词（周围的词）来学习该中心词的表示。FastText的改进之处在于，它不仅使用中心词的表示来进行上下文词的预测，还将每个词拆解为多个子词。每个子词都会贡献到目标词的词向量学习中。
- 在FastText中，每个词向量是由其所有子词向量的总和组成的。这样，FastText不仅能够处理已知的词，还能通过词的子词推测出未登录词的向量表示。
CBOW（Continuous Bag of Words）模型
- 和Word2Vec中的CBOW模型很类似, 不同之处在于, FastText预测标签, 而CBOW模型预测中间词。
- 在CBOW模型中，给定一组上下文词，模型的目标是通过预测目标词来学习词向量。在FastText中，每个上下文词的向量是通过其子词表示来生成的，最后通过加权求和得到整个上下文的表示。
- 与Skip-gram类似，FastText会将上下文词的子词向量加和起来，得到上下文词的最终表示。

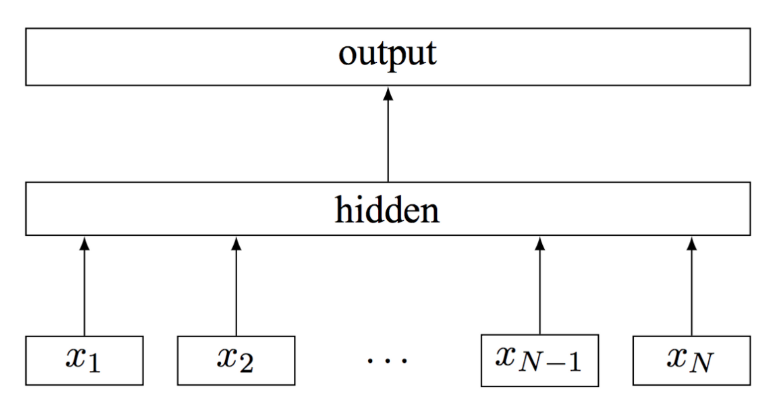
FastText的模型分为三层架构:

输入层: 一系列单词或句子Embedding之后的向量, 包含N-gram特征。
隐藏层: 每个词通过子词建模得到词向量，将文本中的所有词的词向量进行平均，作为文本表示，是对输入数据的求和平均。
输出层: 分类器进行预测，是文档对应的label。

2.2 层次softmax¶

层次softmax（Hierarchical Softmax）是一种用于加速训练的技巧，特别是在处理大规模词汇表时。它通过将 softmax操作转化为一个树形结构（霍夫曼树（Huffman Tree））来减少计算复杂度，从而提升模型的训练效率。

在传统的softmax中，计算目标词的概率需要计算整个词汇表中所有词的概率，这在词汇表非常大的情况下计算开销非常大。层次softmax通过构建一个二叉树，使得每次预测时只需要计算沿路径的几个节点，从而显著降低了计算量。

2.2.1 霍夫曼树介绍¶

层次Softmax通常使用霍夫曼树（Huffman Tree）来构建二叉树。霍夫曼树是一种带权路径长度最短的二叉树，频率高的词在树中的路径较短，频率低的词路径较长，这样可以进一步优化计算效率。

每个词通过霍夫曼编码映射到一条唯一的路径。路径是从根节点到叶子节点的节点序列，路径的长度与词的出现频率成反比：频率高的词路径短，频率低的词路径长。

2.2.2 霍夫曼树相关概念¶

二叉树: 每个节点最多有2个子树的有序树, 两个子树分别称为左子树、右子树。有序的意思是: 树有左右之分, 不能颠倒。
叶子节点: 一棵树当中没有子节点的节点称为叶子节点。
路径和路径长度: 在一棵树中, 从一个节点往下可以到达孩子或孙子节点之间的通路, 称为路径。通路中分支的数目称为路径长度。
节点的权及带权路径长度: 若将树中节点赋予一个有某种含义的数值, 则这个数值称为该节点的权, 节点的带权路径长度为: 从根节点到该节点之间的路径长度与该节点的权的乘积。
树的带权路径长度: 树的带权路径长度规定为所有叶子节点的带权路径长度之和, 记为WPL(weighted path length)。WPL最小的二叉树就是赫夫曼树。

2.2.3 构建霍夫曼树¶

2.2.3.1 构建步骤¶

初始化
- 为每个词汇或符号创建一个叶子节点，节点的权重为词频或概率。
- 将所有节点放入一个优先队列（最小堆），按权重从小到大排序。
合并节点
- 从优先队列中取出权重最小的两个节点。
- 创建一个新的内部节点，其权重为这两个节点权重之和，左子节点为权重较小的节点，右子节点为权重较大的节点。
- 删除从优先队列中取出权重最小的两个节点，将新节点放回优先队列。
重复合并
- 重复步骤2，直到优先队列中只剩一个节点。这个节点就是霍夫曼树的根节点。
生成编码
- 从根节点开始，向左子树走记为0，向右子树走记为1。
- 每个叶子节点的路径即为该符号的霍夫曼编码。

2.2.3.2 示例1¶

假设有以下词汇及其频率：

词汇	频率
A	5
B	9
C	12
D	13
E	16
F	45

步骤1：初始化

创建叶子节点：A(5), B(9), C(12), D(13), E(16), F(45)。
将所有节点放入优先队列（按频率排序）：[A(5), B(9), C(12), D(13), E(16), F(45)]。

步骤2：第一次合并

取出频率最小的两个节点：A(5) 和 B(9)。
创建新节点 N1(14)，左子节点为 A(5)，右子节点为 B(9)。
将 N1(14) 放回优先队列：[C(12), D(13), N1(14), E(16), F(45)]。

步骤3：第二次合并

取出频率最小的两个节点：C(12) 和 D(13)。
创建新节点 N2(25)，左子节点为 C(12)，右子节点为 D(13)。
将 N2(25) 放回优先队列：[N1(14), E(16), N2(25), F(45)]。

步骤4：第三次合并

取出频率最小的两个节点：N1(14) 和 E(16)。
创建新节点 N3(30)，左子节点为 N1(14)，右子节点为 E(16)。
将 N3(30) 放回优先队列：[N2(25), N3(30), F(45)]。

步骤5：第四次合并

取出频率最小的两个节点：N2(25) 和 N3(30)。
创建新节点 N4(55)，左子节点为 N2(25)，右子节点为 N3(30)。
将 N4(55) 放回优先队列：[F(45), N4(55)]。

步骤6：第五次合并

取出频率最小的两个节点：F(45) 和 N4(55)。
创建新节点 N5(100)，左子节点为 F(45)，右子节点为 N4(55)。
优先队列中只剩一个节点 N5(100)，构建完成。

最终霍夫曼树结构：

Python

                N5(100)
             /            \
     F(45)        N4(55)
                        /         \
                N2(25)    N3(30)
                /     \        /     \
         C(12) D(13) N1(14) E(16)
                                 /     \
                            A(5)    B(9)

霍夫曼编码：

从根节点到每个叶子节点的路径即为该词汇的霍夫曼编码：

词汇	路径	编码
F	左	0
C	右 -> 左	100
D	右 -> 右	101
A	右 -> 左	1100
B	右 -> 右	1101
E	右 -> 右	111

2.2.3 层次softmax¶

工作原理:

霍夫曼树: 每个叶子节点代表一个词，每个非叶子节点代表一个二元分类问题。词频高的词在树的较高层，词频低的词在树的较低层。这使得高频词的路径更短，从而减少计算。
路径编码: 从根节点到叶子节点的路径可以被编码为一个二元码 (0 或 1)，其中0代表左子树，1代表右子树。
概率计算: 每个非叶子节点代表一个二元分类问题，使用sigmoid函数计算概率。从根节点到叶子节点的概率是路径上所有节点概率的乘积。

优势:

计算效率高：层次Softmax将计算复杂度从O(V)降低到O(logV)，其中V是词汇量的大小。
内存效率高：只需要存储树的结构和节点的参数，不需要存储整个词汇表的参数。

2.3 负采样¶

2.3.1 什么是负采样¶

负采样（Negative Sampling）是FastText和其他自然语言处理模型（如Word2Vec）中用于加速训练和提高效率的一种技术。它主要用于解决传统Softmax在大词汇量情况下的计算瓶颈问题。负采样通过简化目标函数，只对少数负样本进行更新，从而大幅减少计算量。

2.3.2 负采样原理¶

负采样的核心思想是将多分类问题转化为二分类问题，只更新正样本和少量负样本的参数，而不是整个词汇表。具体来说：

正样本: 对于给定的中心词 \(w_c\)，我们选取其上下文词 \(w_o\) 作为正样本。
负样本: 我们从词汇表中随机选择一些词，作为负样本。这些词与中心词 \(w_c\) 的上下文词无关。
二分类问题: 将每个正样本视为 1，负样本视为 0，训练一个二元分类器来区分中心词和上下文词是否相关。
- 对于正样本，目标是最大化其概率。
- 对于负样本，目标是最小化其概率。

当我们训练一个神经网络意味着要输入训练样本并且不断调整神经元的权重, 从而不断提高对目标的准确预测。每当神经网络经过一个训练样本的训练, 它的权重就会进行一次调整. 比如我们利用Skip-Gram进行词向量的训练, 如果词汇量的数量为上万个, 那么我们利用softmax计算概率时, 需要对计算上万个概率值, 且每个值都需要进行反向传播更新模型参数, 这是非常消耗计算资源的, 并且实际中训练起来会非常慢。

不同于原本每个训练样本更新所有的权重, 负采样每次让一个训练样本仅仅更新一小部分的权重, 这样就会降低梯度下降过程中的计算量。

举例说明（负采样原理）:

当我们用训练样本 ( input word: “hello”, output word: “man”) 来训练我们的神经网络时, “ hello”和“man”都是经过one-hot编码的。如果我们的vocabulary大小为10000时, 在输出层, 我们期望对应“man”单词的那个神经元结点输出1, 其余9999个都应该输出0。在这里, 这9999个我们期望输出为0的神经元结点所对应的单词我们称为“negative” word。
当使用负采样时, 我们将随机选择一小部分的negative words（比如选5个negative words）来更新对应的权重. 我们也会对我们的“positive” word进行权重更新（在我们上面的例子中, 这个单词指的是”man“）。
注意, 对于小规模数据集, 选择5-20个negative words会比较好, 对于大规模数据集可以仅选择2-5个negative words。
假如我们的隐藏层-输出层拥有300 x 10000的权重矩阵。如果使用了负采样的方法我们仅仅去更新我们的positive word-“man”的和我们选择的其他5个negative words的结点对应的权重, 共计6个输出神经元, 相当于每次只更新300×6=1800个权重。对于3百万的权重来说, 相当于只计算了0.06%的权重, 这样计算效率就大幅度提高。

2.3.3 负采样优势¶

负采样的主要优势在于它显著减少了每次参数更新时所需的计算量。具体来说：

减少计算复杂度：在传统的 softmax 中，需要对整个词汇表的每个词计算概率，而负采样只需要计算 \(k\) 个负样本的概率和目标词的概率，因此计算复杂度从 \(O(∣V∣)\) 降到 \(O(k)\)，其中 \(∣V∣\) 是词汇表的大小，\(k\) 是负样本的数量。
内存效率高：由于不需要存储和计算整个词汇表的概率分布，负采样可以显著减少内存消耗。
训练速度快：由于每次训练时只考虑目标词和少数几个负样本，训练速度可以比传统的softmax快很多。

2.4 小结¶

什么是fasttext模型架构:
- fastText模型架构和Word2Vec中的CBOW模型很类似, 不同之处在于, fastText预测标签, 而CBOW模型预测中间词
什么是层次softmax:
- 为了提高效率, 在fastText中计算分类标签概率的时候, 不再使用传统的softmax来进行多分类的计算, 而是使用哈夫曼树, 使用层次化的softmax来进行概率的计算
霍夫曼树定义:
- 当利用n个结点试图构建一棵树时, 如果构建的这棵树的带权路径长度最小, 称这棵树为“最优二叉树”, 有时也叫“赫夫曼树”或者“哈夫曼树”
优点:
- 传统的softmax的时间复杂度为L(labels的数量), 但是使用层次化softmax之后时间复杂度的log(L) (二叉树的高度和宽度的近似), 从而在多分类的场景提高了效率
负采样:
- 负采样原理:
  - 负采样每次让一个训练样本仅仅更新一小部分的权重, 这样就会降低梯度下降过程中的计算量
- 优点:
  - 提高训练速度, 选择了部分数据进行计算损失, 损失计算更加简单
  - 改进效果, 增加部分负样本, 能够模拟真实场景下的噪声情况, 能够让模型的稳健性更强