3 输入部分实现¶
学习目标¶
- 了解文本嵌入层和位置编码的作用
- 掌握文本嵌入层和位置编码的实现过程
3.1 输入部分介绍¶
输入部分包含:
-
编码器源文本嵌入层及其位置编码器
-
解码器目标文本嵌入层及其位置编码器
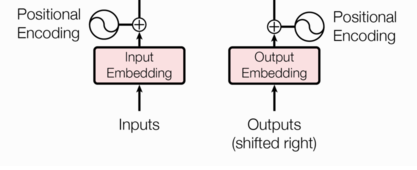
在transformer的encoder和decoder的输入层中,使用了Positional Encoding,使得最终的输入满足:
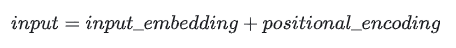
这里,input_embedding是通过常规embedding层,将每一个词的向量维度从vocab_size映射到d_model,由于是相加关系,自然而然地,这里的positional_encoding也是一个d_model维度的向量。(在原论文里,d_model=512)
3.2 文本嵌入层¶
文本嵌入层(Text Embedding Layer)是深度学习模型中将文本(通常是单词或句子)转换为固定大小的向量表示的一个关键层。它的目标是将每个文本单元(如单词或子词)映射到一个高维空间中,以便模型能够更好地捕捉到词汇的语义信息和语法信息。
无论是源文本嵌入还是目标文本嵌入,都是为了将文本中词汇的数字表示转变为向量表示, 希望在这样的高维空间捕捉词汇间的关系。常见的词嵌入方法包括:Word2Vec, GloVe, FastText, 以及可学习的embedding层。
nn.Embedding演示:
embedding = nn.Embedding(num_embeddings=10, embedding_dim=3)
input = torch.LongTensor([[1, 2, 4, 5], [4, 3, 2, 9]])
print(embedding(input))
# padding_idx: 指定用于填充的索引。如果设置为0,则索引为0的输入将始终映射到一个全零向量,并且在反向传播时不会更新该嵌入。
# 全零向量:padding_idx 指定的索引(如0)会被映射到一个全零向量。
# 不更新梯度:在训练过程中,padding_idx 对应的嵌入向量不会被更新。
# 用途:常用于处理变长序列的填充部分,避免填充部分对模型训练产生影响。
embedding = nn.Embedding(num_embeddings=10, embedding_dim=3, padding_idx=0)
input = torch.LongTensor([[0, 2, 0, 5]])
print(embedding(input))
输出结果:
tensor([[[-1.0378, 0.0594, 2.6601],
[ 1.0423, -0.4094, 0.3436],
[-1.8989, 1.3664, -0.3701],
[ 0.3930, 0.9908, 1.5700]],
[[-1.8989, 1.3664, -0.3701],
[ 0.3479, -0.2118, -0.1244],
[ 1.0423, -0.4094, 0.3436],
[ 0.4161, 0.4799, -0.4094]]], grad_fn=<EmbeddingBackward0>)
tensor([[[ 0.0000, 0.0000, 0.0000],
[-0.3378, 1.1013, -1.7552],
[ 0.0000, 0.0000, 0.0000],
[ 0.9153, 0.3548, 2.1857]]], grad_fn=<EmbeddingBackward0>)
文本嵌入层的代码实现:
# 导入必备的工具包
import torch
# 预定义的网络层torch.nn, 工具开发者已经帮助我们开发好的一些常用层,
# 比如,卷积层, lstm层, embedding层等, 不需要我们再重新造轮子.
import torch.nn as nn
# 数学计算工具包
import math
# Embeddings类 实现思路分析
# 1 init函数 (self, d_model, vocab)
# 设置类属性 定义词嵌入层 self.lut层
# 2 forward(x)函数
# self.lut(x) * math.sqrt(self.d_model)
class Embeddings(nn.Module):
def __init__(self, vocab, d_model):
# 参数vocab 词汇表大小
# 参数d_model 每个词汇的特征尺寸 词嵌入维度
super(Embeddings, self).__init__()
self.vocab = vocab
self.d_model = d_model
# 定义词嵌入层
self.embed = nn.Embedding(self.vocab, self.d_model)
def forward(self, x):
# 将x传给self.embed并与根号下self.d_model相乘作为结果返回
# 词嵌入层的权重通常初始化较小(如均匀分布在[-0.1, 0.1]), 导致嵌入后的向量幅度较小。
# x经过词嵌入后乘以sqrt(d_model)来增大x的值, 与位置编码信息值量纲[-1,1]差不多, 确保两者相加时信息平衡。
return self.embed(x) * math.sqrt(self.d_model)
调用:
def dm_test_Embeddings():
vocab = 1000 # 词表大小是1000
d_model = 512 # 词嵌入维度是512维
# 实例化词嵌入层
my_embeddings = Embeddings(vocab, d_model)
x = torch.LongTensor([[100, 2, 421, 508], [491, 998, 1, 221]])
embed = my_embeddings(x)
print('embed.shape', embed.shape, '\nembed--->\n', embed)
if __name__ == '__main__':
dm_test_Embeddings()
输出结果:
embed.shape torch.Size([2, 4, 512])
embed--->
tensor([[[ -0.9264, -38.2338, 18.5574, ..., 36.3375, -20.2969, 6.8429],
[ 14.1119, -5.2766, 1.8418, ..., 20.2530, -21.8190, -0.3868],
[-28.7141, 15.6517, 7.0343, ..., -24.7212, 11.7169, 9.1018],
[ 25.7579, 23.5704, 6.5489, ..., 2.7449, -0.5301, 15.3012]],
[[-18.3689, -23.4577, -10.3820, ..., 6.2848, -3.8342, -2.2106],
[ 41.2917, 26.6871, 21.3547, ..., -21.6043, -14.3414, -5.8511],
[-42.9315, -6.7251, -3.0975, ..., -8.0635, -37.7340, 4.6406],
[ -1.2356, 22.7560, -28.8711, ..., 56.8816, -12.9638, 0.5119]]],
grad_fn=<MulBackward0>)
3.3 位置编码器¶
位置编码器(Positional Encoding)是Transformer模型中的一个重要组成部分,用于在模型中引入序列中各个元素的位置或顺序信息。因为在Transformer的编码器结构中, 并没有RNN那样针对词汇位置信息的处理能力,它无法直接感知输入数据中的顺序关系。因此需要在Embedding层后加入位置编码器,将词汇位置不同可能会产生不同语义的信息加入到词嵌入张量中, 以弥补位置信息的缺失。
位置编码器将序列位置(例如,单词在句子中的位置)转换为一组向量,这些向量会与输入的词嵌入(word embeddings)相加,使模型能够在处理每个词时,理解其在序列中的位置。
位置编码通常使用正弦和余弦函数生成,使得模型可以区分不同位置的token。
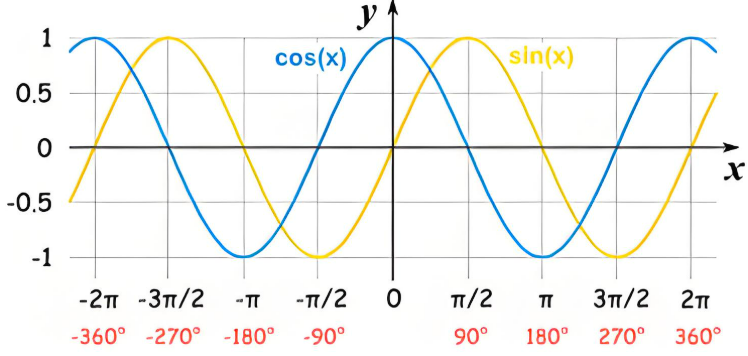
在Transformer中,位置编码的公式是:
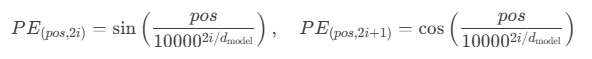
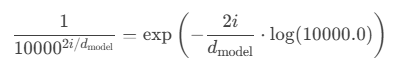
其中:
- \(pos\) 是词在序列中的实际位置(例如第1个词为0,第2个词为1…)
- \(i\) 是维度索引,每个词向量维度下标值
- \(d_{model}\) 是模型的维度,也是词向量维度
正弦和余弦函数特点:
-
周期性
-
正弦和余弦函数是周期性的,它们的周期是2π,可以自然地表示位置之间的相对关系。
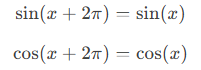
-
对于两个位置pos和pos+k,它们的位置编码可以通过正弦和余弦函数的周期性关系直接关联起来。
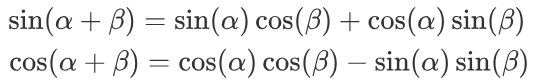
-
例如“位置pos+k是位置pos的下一个位置”。它们的位置编码之间存在一种线性关系:
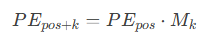
其中Mk是一个与位置偏移k相关的线性变换矩阵,这种关联性使得模型能够轻松地学习到位置之间的相对关系。
-
在句子“The cat sat on the mat”中,单词“sat”与“cat”之间的关系(相邻)比它们的绝对位置(第2个和第3个词)更重要。
-
-
平滑性
- 正弦和余弦函数是平滑的,能够捕捉到位置的连续变化。
- 在正弦和余弦函数中,斜率也是连续变化的,函数的导数(即变化的速率)在所有地方都存在并且是平滑的。
-
有界性
- 正弦和余弦函数的值域在
[-1, 1]之间,避免了数值爆炸问题。 - 输出范围可控,位置编码的值不会过大或过小,避免了数值不稳定性。
- 正弦和余弦函数的值域在
位置编码器的代码实现:
# 位置编码器类PositionalEncoding 实现思路分析
# 1 init函数 (self, d_model, dropout_p, max_len=5000)
# super()函数 定义层self.dropout
# 定义位置编码矩阵pe 定义位置列-矩阵position 定义变化矩阵div_term
# 套公式div_term = torch.exp(-torch.arange(0, d_model, 2) / d_model * math.log(10000.0))
# 位置列-矩阵 * 变化矩阵 阿达码积my_matmulres
# 给pe矩阵偶数列奇数列赋值 pe[:, 0::2] pe[:, 1::2]
# pe矩阵注册到模型缓冲区 pe.unsqueeze(0)三维 self.register_buffer('pe', pe)
# 2 forward(self, x) 返回self.dropout(x)
# 给x数据添加位置特征信息 x = x + self.pe[:,:x.shape[1], :]
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout_p, max_len=5000):
# 参数d_model 词嵌入维度 eg: 512个特征
# 参数max_len 单词token个数 eg: 60个单词
super(PositionalEncoding, self).__init__()
# 定义dropout层
self.dropout = nn.Dropout(p=dropout_p)
# 思路:位置编码矩阵 + 特征矩阵 相当于给特征增加了位置信息
# 定义位置编码矩阵PE eg pe[60, 512], 位置编码矩阵和特征矩阵形状是一样的
pe = torch.zeros(max_len, d_model)
# 定义位置列-矩阵position 数据形状[max_len,1] eg: [0,1,2,3,4...60]^T
position = torch.arange(0, max_len).unsqueeze(1)
# print('position--->', position.shape, position)
# 方式一计算
# _2i = torch.arange(0, d_model, step=2).float()
# pe[:, 0::2] = torch.sin(position / 10000 ** (_2i / d_model))
# pe[:, 1::2] = torch.cos(position / 10000 ** (_2i / d_model))
# 方式二计算
# 定义变化矩阵div_term [1,256]
# torch.arange(start=0, end=512, 2)结果并不包含end。在start和end之间做一个等差数组 [0, 2, 4, 6 ... 510]
# math.log(10000.0)对常数10000取自然对数
# torch.exp()指数运算
div_term = torch.exp(-torch.arange(0, d_model, 2) / d_model * math.log(10000.0))
# 位置列-矩阵 @ 变化矩阵 做矩阵运算 [60*1]@ [1*256] ==> 60*256
# 矩阵相乘也就是行列对应位置相乘再相加,其含义,给每一个列属性(列特征)增加位置编码信息
my_matmulres = position * div_term
# print('my_matmulres--->', my_matmulres.shape, my_matmulres)
# 给位置编码矩阵奇数列,赋值sin曲线特征
pe[:, 0::2] = torch.sin(my_matmulres)
# 给位置编码矩阵偶数列,赋值cos曲线特征
pe[:, 1::2] = torch.cos(my_matmulres)
# 形状变化 [60,512]-->[1,60,512]
pe = pe.unsqueeze(0)
# 把pe位置编码矩阵 注册成模型的持久缓冲区buffer; 模型保存再加载时,可以根模型参数一样,一同被加载
# 什么是buffer: 对模型效果有帮助的,但是却不是模型结构中超参数或者参数,不参与模型训练
self.register_buffer('pe', pe)
def forward(self, x):
# 注意:输入的x形状2*4*512 pe形状1*60*512 如何进行相加
# 只需按照x的单词个数 给特征增加位置信息
x = x + self.pe[:, :x.shape[1], :]
return self.dropout(x)
调用:
def dm_test_PositionalEncoding():
vocab = 1000 # 词表大小是1000
d_model = 512 # 词嵌入维度是512维
# 1 实例化词嵌入层
my_embeddings = Embeddings(vocab, d_model)
# 2 让数据经过词嵌入层 [2,4] --->[2,4,512]
x = torch.LongTensor([[100, 2, 421, 508], [491, 998, 1, 221]])
embed = my_embeddings(x)
# print('embed--->', embed.shape)
# 3 创建pe位置矩阵 生成位置特征数据[1,60,512]
my_pe = PositionalEncoding(d_model=d_model, dropout_p=0.1, max_len=60)
# 4 给词嵌入数据embed 添加位置特征 [2,4,512] ---> [2,4,512]
pe_result = my_pe(embed)
print('pe_result.shape--->', pe_result.shape)
print('pe_result--->', pe_result)
if __name__ == '__main__':
dm_test_PositionalEncoding()
输出结果:
pe_result.shape---> torch.Size([2, 4, 512])
pe_result---> tensor([[[-31.7233, 7.1880, -35.8665, ..., -0.0000, -8.7751, -39.0546],
[ -8.1961, -5.8707, 6.6460, ..., 41.9253, -10.8338, -0.0000],
[ 13.6579, 11.7870, 39.9218, ..., 0.0000, 10.1335, 11.4966],
[-10.0956, -4.7150, -27.5220, ..., -7.3646, -40.9978, 13.9090]],
[[-31.8694, 33.0375, 15.3635, ..., 14.1677, 13.7319, -5.1402],
[ 14.0821, 26.6213, -6.8929, ..., -6.5874, 1.0178, 9.6971],
[-27.0425, 25.3489, 27.7457, ..., 0.0000, 10.3564, 1.5655],
[-21.3439, -12.2684, -56.1276, ..., 13.8567, 0.0000, -0.0000]]],
grad_fn=<MulBackward0>)
绘制词汇向量中特征的分布曲线:
import matplotlib.pyplot as plt
import numpy as np
# 绘制PE位置特征sin-cos曲线
def dm_draw_PE_feature():
# 1 创建pe位置矩阵[1,5000,20],每一列数值信息:奇数列sin曲线 偶数列cos曲线
my_pe = PositionalEncoding(d_model=20, dropout_p=0)
print('my_positionalencoding.shape--->', my_pe.pe.shape)
# 2 创建数据x[1,100,20], 给数据x添加位置特征 [1,100,20] ---> [1,100,20]
y = my_pe(torch.zeros(1, 100, 20))
print('y--->', y.shape)
# 3 画图 绘制pe位置矩阵的第4-7列特征曲线
plt.figure(figsize=(20, 10))
# 第0个句子的,所有单词的,绘制4到8维度的特征 看看sin-cos曲线变化
plt.plot(np.arange(100), y[0, :, 4:8].numpy())
plt.legend(["dim %d" % p for p in [4, 5, 6, 7]])
plt.show()
# print('直接查看pe数据形状--->', my_pe.pe.shape) # [1,5000,20]
# 直接绘制pe数据也是ok
# plt.figure(figsize=(20, 20))
# # 第0个句子的,所有单词的,绘制4到8维度的特征 看看sin-cos曲线变化
# plt.plot(np.arange(100), my_pe.pe[0,0:100, 4:8])
# plt.legend(["dim %d" %p for p in [4,5,6,7]])
# plt.show()
if __name__ == '__main__':
dm_draw_PE_feature()
输出结果:
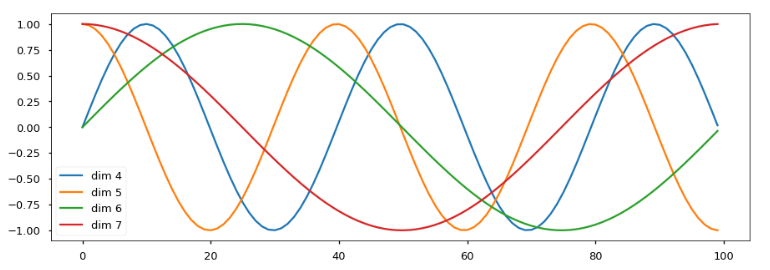
效果分析:
- 每条颜色的曲线代表某一个词汇中的特征在不同位置的含义
- 保证同一词汇随着所在位置不同它对应位置嵌入向量会发生变化
- 正弦波和余弦波的值域范围都是1到-1这又很好的控制了嵌入数值的大小, 有助于梯度的快速计算
3.4 小结¶
- 文本嵌入层的作用:
- 无论是源文本嵌入还是目标文本嵌入,都是为了将文本中词汇的数字表示转变为向量表示, 希望在这样的高维空间捕捉词汇间的关系.
- 文本嵌入层的类: Embeddings
- 初始化函数以d_model, 词嵌入维度, 和vocab, 词汇总数为参数, 内部主要使用了nn中的预定层Embedding进行词嵌入.
- 在forward函数中, 将输入x传入到Embedding的实例化对象中, 然后乘以一个根号下d_model进行缩放, 控制数值大小.
- 它的输出是文本嵌入后的结果.
- 位置编码器的作用:
- 因为在Transformer的编码器结构中, 并没有针对词汇位置信息的处理,因此需要在Embedding层后加入位置编码器,将词汇位置不同可能会产生不同语义的信息加入到词嵌入张量中, 以弥补位置信息的缺失.
- 位置编码器的类: PositionalEncoding
- 初始化函数以d_model, dropout_p, max_len为参数, 分别代表d_model: 词嵌入维度, dropout_p: 置0概率, max_len: 每个句子的最大长度.
- forward函数中的输入参数为x, 是Embedding层的输出.
- 最终输出一个加入了位置编码信息的词嵌入张量.
- 绘制词汇向量中特征的分布曲线:
- 保证同一词汇随着所在位置不同它对应位置嵌入向量会发生变化.
- 正弦波和余弦波的值域范围都是1到-1, 这又很好的控制了嵌入数值的大小, 有助于梯度的快速计算.