3 LSTM模型¶

学习目标¶

了解LSTM内部结构及计算公式
掌握Pytorch中LSTM工具的使用
了解LSTM的优势与缺点

3.1 LSTM介绍¶

LSTM（Long Short-Term Memory）也称为长短期记忆网络，是一种改进的循环神经网络（RNN），专门设计用于解决传统RNN的梯度消失问题和长程依赖问题。LSTM通过引入门机制和细胞状态，能够更好地捕捉长序列数据中的长期依赖关系。

它的核心思想是通过引入门机制（输入门、遗忘门、输出门）和细胞状态（Cell State）来控制信息的流动，从而决定哪些信息需要保留、哪些信息需要丢弃。

3.1.1 内部结构¶

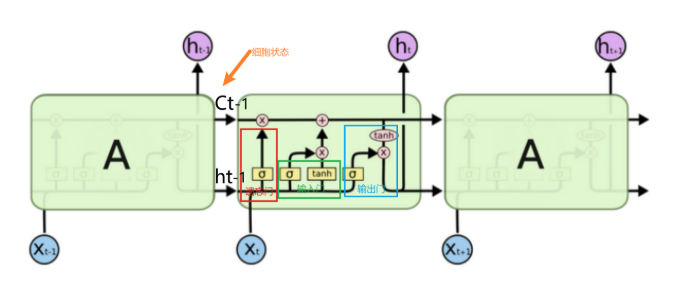
1749048674326

遗忘门：决定了哪些信息应该被丢弃（即遗忘）。它读取当前输入和前一时刻的隐藏状态，然后输出一个0到1之间的数值，表示当前时刻的信息应当保留或丢弃的比例。

输入门：决定了哪些信息需要被存储到当前的单元状态中。通过这个门来更新单元状态的记忆。

细胞状态：可以将其视为一条贯穿整个网络的”传送带”，携带长期记忆；信息通过细胞状态传递，并由各个门控机制选择性地修改。

输出门：控制从单元状态到隐藏状态的信息流出，决定当前的隐藏状态输出多少细胞状态的内容。

① 细胞状态（Cell State）

作用：细胞状态\(C_t\)是LSTM核心，用于存储长期信息
特点：
- 细胞状态在整个时间步中传递，只有少量的线性交互
- 通过门机制更新细胞状态

② 遗忘门（Forget Gate）

作用：决定哪些信息从细胞状态中丢弃
公式：

\(f_t=σ(W_f⋅[h_{t−1},x_t]+b_f)\)
- \(f_t\)：遗忘门的输出（0表示完全丢弃，1表示完全保留）
- \(W_f\),\(b_f\)：权重矩阵和偏置项
- \(σ\)：\(Sigmoid\)激活函数

③ 输入门（Input Gate）

作用：决定哪些新信息存储到细胞状态中
公式：

\(i_t=σ(Wi⋅[h_{t−1},x_t]+b_i)\)
- \(i_t\)：输入门的输出（0 到 1 之间的值）
- \(W_i\),\(b_i\)：权重矩阵和偏置项
- \(σ\)：\(Sigmoid\)激活函数

④ 候选细胞状态（Candidate Cell State）

作用：生成新的候选值，用于更新细胞状态
公式：

\(\tilde{C}_t=tanh⁡(W_C⋅[h_{t−1},x_t]+b_C)\)
- \(\tilde{C}_t\)：候选细胞状态
- \(W_C\),\(b_C\)：权重矩阵和偏置项
- \(tanh\)⁡：双曲正切激活函数

⑤ 更新细胞状态

作用：细胞状态 \(C_t\) 是LSTM的记忆，结合遗忘门和输入门，更新细胞状态
公式：

\(C_t=f_t⋅C_{t−1}+i_t⋅\tilde{C}_t\)
- \(C_t\)：更新后的细胞状态
- 遗忘门\(f_t\): 决定了上一时刻的细胞状态 \(C_{t-1}\) 中保留多少信息
- 输入门\(i_t\): 决定了当前时刻输入 \(x_t\) 中有多少新信息被添加到细胞状态中

⑥ 输出门（Output Gate）

作用：决定细胞状态的哪些部分输出到隐藏状态
公式：

\(o_t=σ(W_o⋅[h_{t−1},x_t]+b_o)\)
- \(o_t\)：输出门的输出（0 到 1 之间的值）
- \(W_o,b_o\)：权重矩阵和偏置项
- \(σ\)：\(Sigmoid\)激活函数

⑦ 隐藏状态（Hidden State）

作用：作为LSTM的输出，传递到下一个时间步
公式：

\(h_t=o_t⋅tanh⁡(C_t)\)
- \(h_t\)：当前时间步的隐藏状态
- \(C_t\)：是当前时刻的细胞状态

3.2 LSTM的内部结构图¶

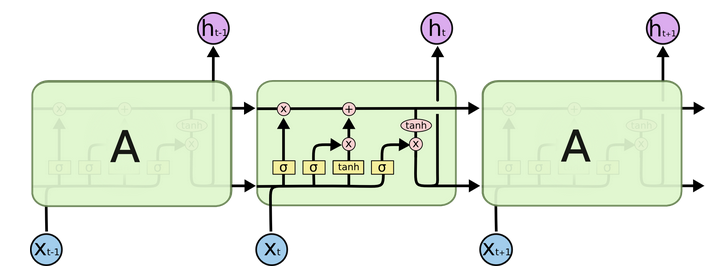
结构解释图:

3.2.1 遗忘门¶

遗忘门部分结构图与计算公式:
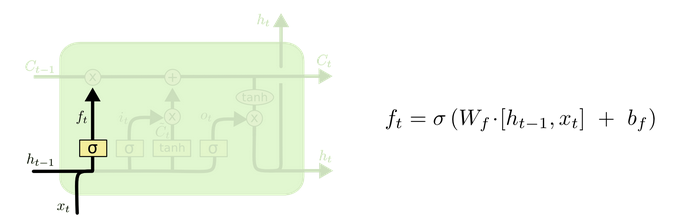
遗忘门结构分析:

与传统RNN的内部结构计算非常相似，首先将当前时间步输入\(x_t\)与上一个时间步隐藏状态\(h_{t-1}\)拼接，得到[\(x_t\)，\(h_{t-1}\)]，然后通过一个全连接层做变换，最后通过\(sigmoid\)函数进行激活得到\(f_t\)。我们可以将\(f_t\)看作是门值，好比一扇门开合的大小程度，门值都将作用在通过该扇门的张量上，遗忘门门值将作用在上一层的细胞状态上，代表遗忘过去的多少信息，又因为遗忘门门值是由\(x_t\)，\(h_{t-1}\)计算得来的，因此整个公式意味着根据当前时间步输入和上一个时间步隐藏状态\(h_{t-1}\)来决定遗忘多少上一层的细胞状态所携带的过往信息。

遗忘门内部结构过程演示:
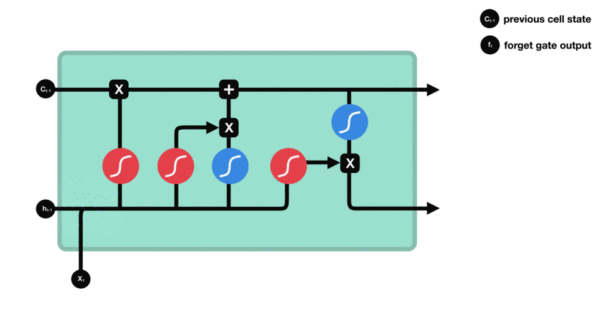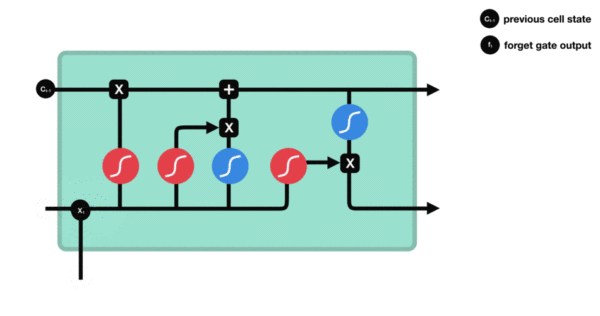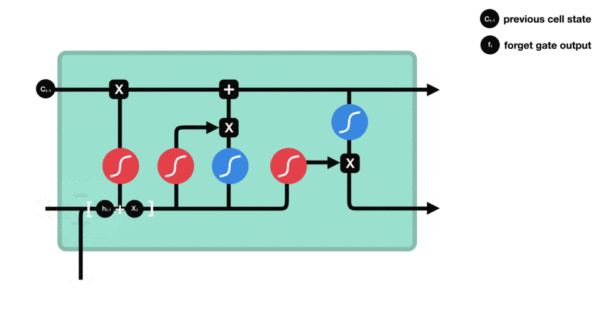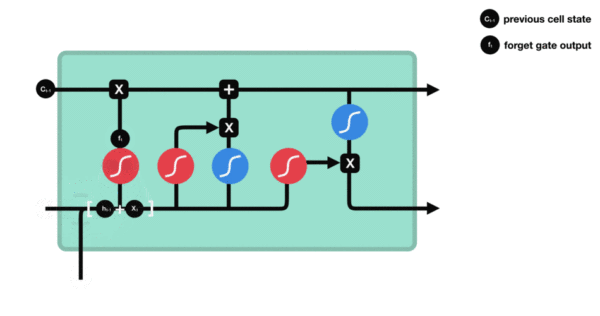
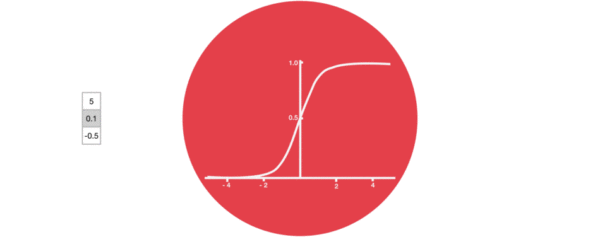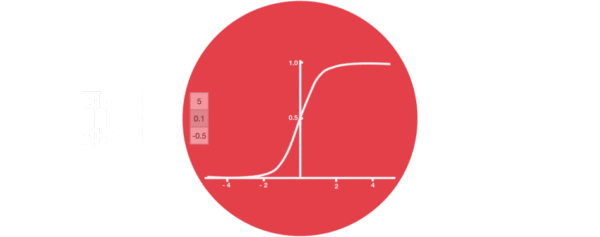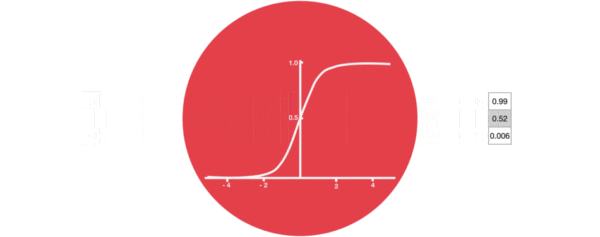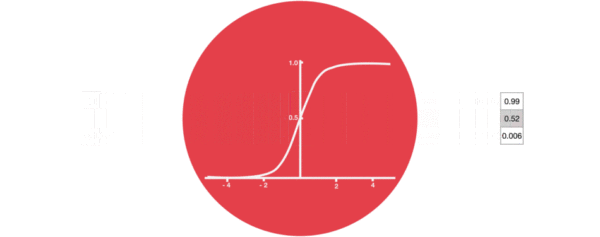
激活函数sigmiod的作用：用于帮助调节流经网络的值, sigmoid函数将值压缩在0和1之间。

3.2.2 输入门¶

输入门部分结构图与计算公式:
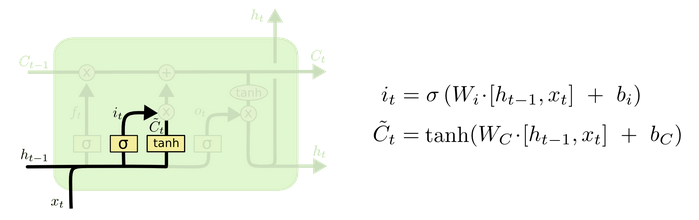
输入门结构分析:

我们看到输入门的计算公式有两个，第一个就是产生输入门门值的公式，它和遗忘门公式几乎相同，区别只是在于它们之后要作用的目标上。这个公式意味着输入信息有多少需要进行过滤，输入门的第二个公式是与传统RNN的内部结构计算相同。对于LSTM来讲，它得到的是当前的细胞状态，而不是像经典RNN一样得到的是隐藏状态。

输入门内部结构过程演示:

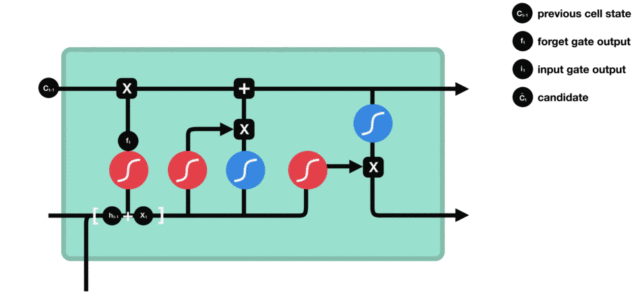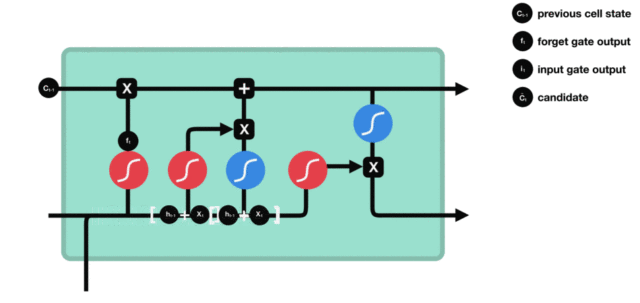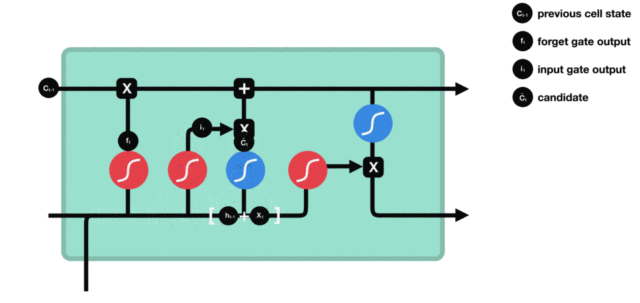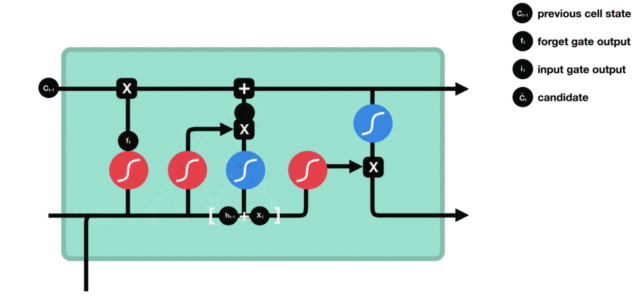
3.2.3 细胞状态¶

细胞状态更新图与计算公式:
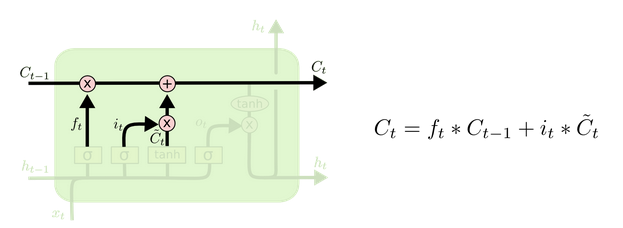
细胞状态更新分析:

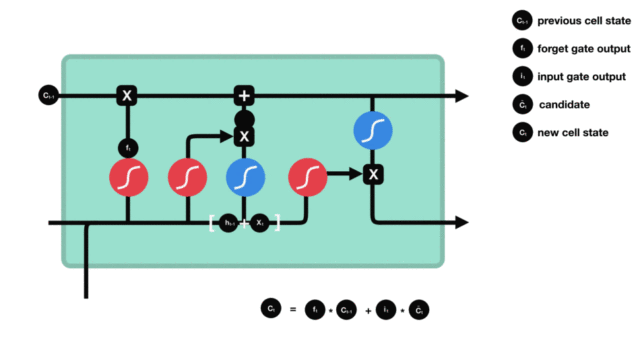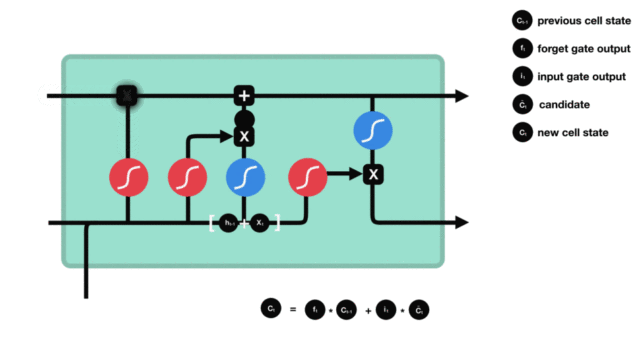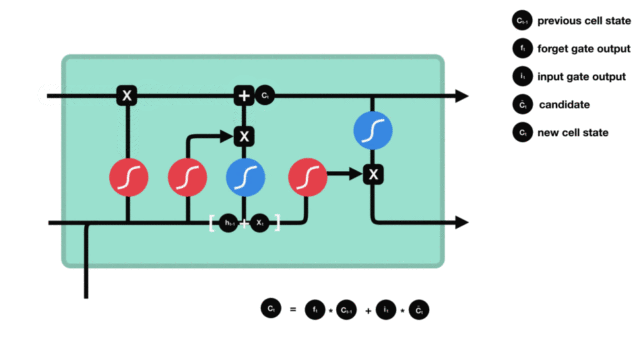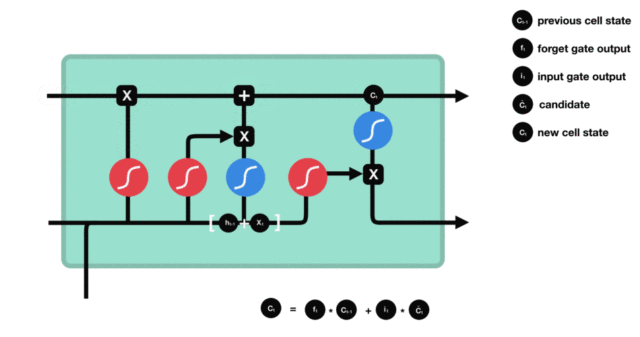
细胞更新的结构与计算公式非常容易理解，这里没有全连接层，只是将刚刚得到的遗忘门门值与上一个时间步得到的\(C_{t-1}\)相乘，再加上输入门门值与当前时间步得到的未更新\(C_t\)相乘的结果。最终得到更新后的\(C_t\)作为下一个时间步输入的一部分。整个细胞状态更新过程就是对遗忘门和输入门的应用。

细胞状态更新过程演示：

3.2.4 输出门¶

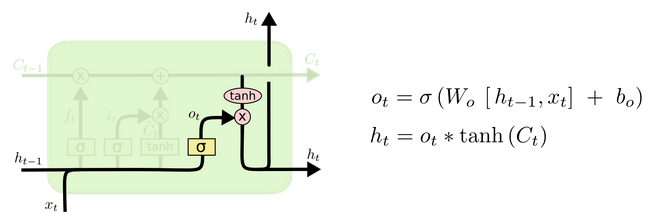
输出门部分结构图与计算公式:
输出门结构分析:

输出门部分的公式也是两个，第一个即是计算输出门的门值，它和遗忘门、输入门计算方式相同。第二个即是使用这个门值产生隐藏状态\(h_t\)，它将作用在更新后的细胞状态\(C_t\)上，并做\(tanh\)激活，最终得到\(h_t\)作为下一时间步输入的一部分。整个输出门的过程，就是为了产生隐藏状态\(h_t\)。

输出门内部结构过程演示:

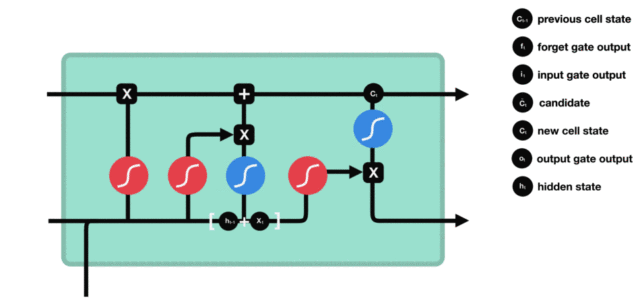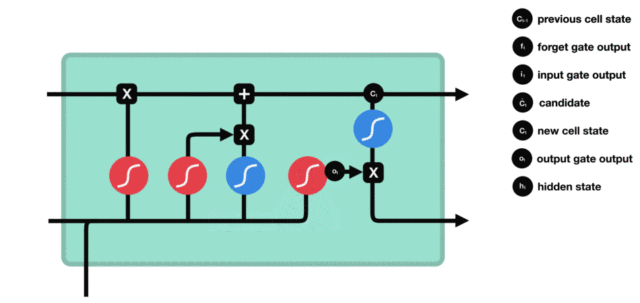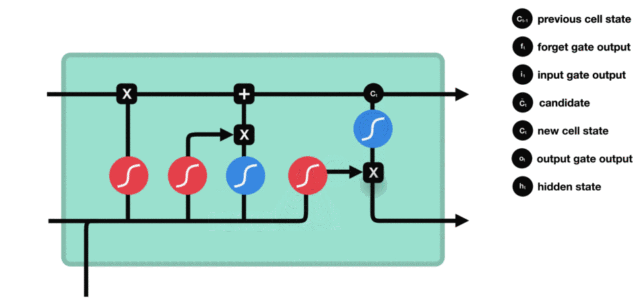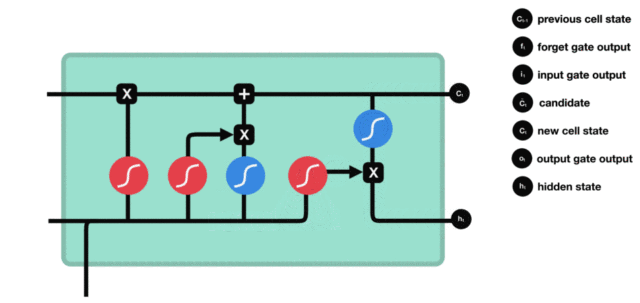
3.3.5 LSTM工作流程¶

遗忘门：
- 根据当前输入 \(x_t\) 和前一隐藏状态 \(h_{t−1}\)，决定细胞状态 \(C_{t−1}\) 中哪些信息需要丢弃。
输入门：
- 根据当前输入 \(x_t\) 和前一隐藏状态 \(h_{t−1}\)，决定哪些新信息需要添加到细胞状态中。
更新细胞状态：
- 结合遗忘门和输入门的结果，更新细胞状态 \(C_t\)。
输出门：
- 根据当前输入 \(x_t\) 和前一隐藏状态 \(h_{t−1}\)，决定细胞状态 \(C_t\) 中哪些信息需要输出。
生成隐藏状态：
- 根据输出门的结果和更新后的细胞状态，生成当前时间步的隐藏状态 \(h_t\)。

3.3 Bi-LSTM介绍¶

Bi-LSTM（双向长短期记忆网络，Bidirectional Long Short-Term Memory Network）是一种扩展版的LSTM（长短期记忆网络），它通过结合正向LSTM和反向LSTM来捕捉序列数据的上下文信息。与传统的单向LSTM（仅从过去到现在的时间序列建模）不同，Bi-LSTM能够同时从过去和未来的上下文信息中学习，从而提高模型的表现，尤其在需要了解整个序列上下文的任务中非常有效。它没有改变LSTM本身任何的内部结构，只是将LSTM应用两次且方向不同，再将两次得到的LSTM结果进行拼接作为最终输出。

Bi-LSTM的核心思想是通过两个独立的LSTM层分别处理序列的正向和反向信息，然后将两个方向的隐藏状态结合起来，生成最终的输出。

正向LSTM：从序列的开始到结束处理数据。
反向LSTM：从序列的结束到开始处理数据。

通过结合正向和反向的信息，Bi-LSTM能够同时捕捉过去和未来的上下文信息。

3.3.1 内部结构¶

输入层：将输入序列传递给两个LSTM网络（正向和反向）。

正向LSTM：按照时间顺序处理输入序列（从第一个时间步到最后一个时间步）。

反向LSTM：逆序处理输入序列（从最后一个时间步到第一个时间步）。

合并层：正向和反向LSTM的输出通常被拼接在一起，形成一个包含更多上下文信息的表示。

输出层：将合并后的表示传递到下游任务，进行分类、回归或者其他任务的预测。

① 正向 LSTM

输入：序列的正向数据 \(x_1,x_2,…,x_T\)。
隐藏状态：\(\overrightarrow{h_t}\)。
细胞状态：\(\overrightarrow{C_t}\)。

② 反向 LSTM

输入：序列的反向数据 \(x_T,x_{T−1},…,x_1\)。
隐藏状态：\(\overleftarrow{h_t}\)。
细胞状态：\(\overleftarrow{C_t}\)。

③ 结合正向和反向信息

将正向和反向的隐藏状态拼接起来，生成最终的隐藏状态：

\(h_t=[\overrightarrow{h_t},\overleftarrow{h_t}]\)
最终的隐藏状态 \(ht\) 包含了序列的完整上下文信息。
\(,\)：表示拼接操作。

④ 输出层：

将双向隐藏状态输入到输出层，得到最终的输出 \(y_1, y_2, ..., y_T\)。
输出层可以是线性层、softmax层等，根据具体任务而定。

Python

正向 LSTM:
输入: x1 -> x2 -> x3 -> ... -> xT
            |         |         |                     |
            v         v         v                     v
LSTM: h1 -> h2 -> h3 -> ... -> hT

反向 LSTM:
输入: xT -> xT-1 -> xT-2 -> ... -> x1
            |            |             |                         |
            v            v             v                         v
LSTM: hT -> hT-1 -> hT-2 -> ... -> h1

结合:
h1 = [h1_forward, h1_backward]
h2 = [h2_forward, h2_backward]
...
hT = [hT_forward, hT_backward]

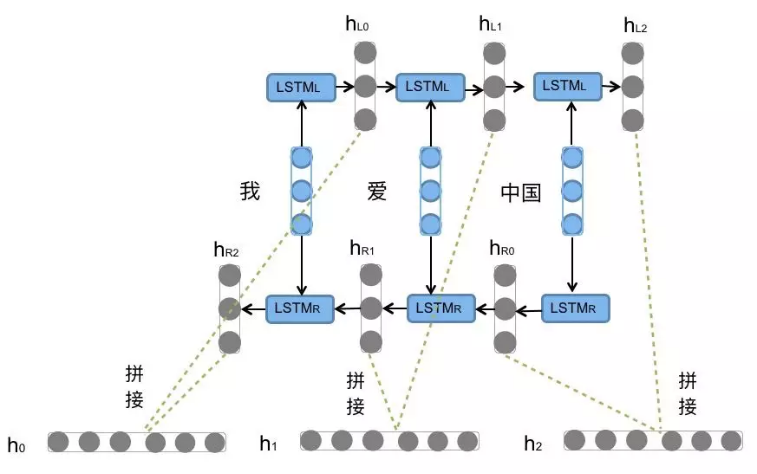
3.3.2 Bi-LSTM的优点¶

捕捉上下文信息：通过结合正向和反向的信息，Bi-LSTM能够更好地捕捉序列的上下文依赖关系
适用于需要全局信息的任务：在自然语言处理（NLP）等任务中，Bi-LSTM能够同时考虑过去和未来的信息
性能优于单向LSTM：在许多任务中，Bi-LSTM的表现优于单向LSTM

3.3.3 Bi-LSTM的缺点¶

计算复杂度高：Bi-LSTM需要同时计算正向和反向的LSTM，计算量是单向LSTM的两倍
参数量大：Bi-LSTM的参数比单向LSTM多，训练时间较长
难以并行化：与LSTM类似，Bi-LSTM需要按时间步依次计算

3.4 Pytorch构建LSTM模型¶

3.4.1 LSTM函数¶

pyTorch中的LSTM实现通过torch.nn.LSTM类提供，如下：

Python

lstm = nn.LSTM(input_size, hidden_size, num_layers, bidirectional, batch_first, dropout)

主要参数介绍如下：

input_size: 输入特征维度，词嵌入维度
hidden_size: 隐藏层特征维度（即每个时间步输出的h_t的维度）
num_layers: LSTM堆叠的层数（默认1层）
bias: 是否使用偏置项（默认True）
batch_first: 输入/输出张量的第一个维度是否为batch_size（默认False，即seq_len在前）
dropout: 非最后一层的LSTM层输出上应用的dropout概率（默认0，即无dropout）
bidirectional: 是否使用双向LSTM（默认False）

3.4.2 输入的表示¶

LSTM的输入包含三个关键部分：输入序列x、初始隐藏状态h0和初始细胞状态c0，如果不提供h0和c0，PyTorch会自动将h0和c0初始化为全零张量。

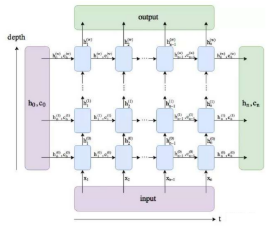
1749048945249

输入序列x的形状为：(seq_len, batch_size, input_size)，具体如下所示：

seq_len: 输入序列的长度, 也就是句子的长度
batch_size: 批次大小, 句子数
input_size: 输入特征维度

初始隐藏状态h0和初始细胞状态c0的形状必须是：(num_layers * num_directions, batch_size, hidden_size)，具体含义如下所示：

num_layers：LSTM的层数
num_directions：1(单向LSTM)或2(双向LSTM)
batch_size：批次大小, 句子数
hidden_size：LSTM的隐藏层维度

双向lstm的层数堆叠如下所示：

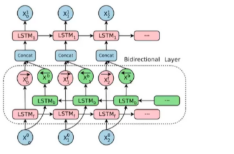
1749048960203

3.4.3 输出的表示¶

LSTM的输出是一个元组(output, (h_n, c_n)):

1.output:

包含LSTM最后一层在所有时间步的隐藏状态

单向LSTM: (seq_len, batch_size, hidden_size)
双向LSTM: (seq_len, batch_size, hidden_size * 2)

2.h_n (隐藏状态):

包含所有层在最后一个时间步的隐藏状态

单向LSTM: (num_layers, batch_size, hidden_size)
双向LSTM: (num_layers * 2, batch_size, hidden_size)

3.c_n (细胞状态):

包含所有层在最后一个时间步的细胞状态
单向LSTM：(num_layers, batch_size, hidden_size)
双向LSTM：(num_layers * 2, batch_size, hidden_size)

3.4.4 LSTM实践¶

Python

# 定义LSTM的参数含义: (input_size, hidden_size, num_layers)
# 定义输入张量的参数含义: (sequence_length, batch_size, input_size)
# 定义隐藏层初始张量和细胞初始状态张量的参数含义: (num_layers * num_directions, batch_size, hidden_size)
import torch.nn as nn
import torch


def dm_lstm():
    # 创建LSTM层
    lstm = nn.LSTM(input_size=5, hidden_size=6, num_layers=2)
    # 创建输入张量
    input = torch.randn(size=(1, 3, 5))
    # 初始化隐藏状态
    h0 = torch.randn(size=(2, 3, 6))
    # 初始化细胞状态
    c0 = torch.randn(size=(2, 3, 6))
        # hn输出两层隐藏状态, 最后1个隐藏状态值等于output输出值
    output, (hn, cn) = lstm(input, (h0, c0))
    print('output--->', output.shape, output)
    print('hn--->', hn.shape, hn)
    print('cn--->', cn.shape, cn)

输出结果:

Python

output---> torch.Size([1, 3, 6]) tensor([[[-0.1221, -0.1894, -0.3486,    0.3517,    0.5493, -0.0260],
                 [ 0.2351,    0.2856,    0.0904,    0.4349, -0.2569,    0.2918],
                 [ 0.0428, -0.2107,    0.1280, -0.1735,    0.1007,    0.0218]]],
             grad_fn=<MkldnnRnnLayerBackward0>)
hn---> torch.Size([2, 3, 6]) tensor([[[-0.1151, -0.0980,    0.0840,    0.0268, -0.1675,    0.0520],
                 [-0.0154,    0.3194,    0.1437, -0.1994, -0.2275, -0.0116],
                 [-0.2031,    0.2344,    0.2544, -0.4311, -0.0562, -0.0250]],

                [[-0.1221, -0.1894, -0.3486,    0.3517,    0.5493, -0.0260],
                 [ 0.2351,    0.2856,    0.0904,    0.4349, -0.2569,    0.2918],
                 [ 0.0428, -0.2107,    0.1280, -0.1735,    0.1007,    0.0218]]],
             grad_fn=<StackBackward0>)
cn---> torch.Size([2, 3, 6]) tensor([[[-0.1606, -0.1351,    0.1162,    0.0392, -0.5632,    0.0839],
                 [-0.0278,    1.1598,    0.2844, -0.3407, -0.5864, -0.0218],
                 [-0.3315,    0.5471,    0.4775, -1.1170, -0.2076, -0.0335]],

                [[-0.2796, -0.3959, -0.6758,    0.5708,    0.9945, -0.0787],
                 [ 0.7208,    0.5018,    0.5595,    1.1216, -0.5735,    0.4760],
                 [ 0.0819, -0.4503,    0.2563, -0.2838,    0.1403,    0.0586]]],
             grad_fn=<StackBackward0>)

3.5 LSTM的优缺点¶

3.5.1 LSTM的优点¶

能够捕捉长期依赖：通过门控机制，LSTM能够记住长期的依赖关系，解决了传统RNN无法记住长期信息的问题。
避免梯度消失
- 细胞状态 \(C_t\) 的更新公式中，\(C_{t−1}\) 和 \(C_t\) 之间是线性关系（通过遗忘门 \(f_t\) 控制）
- LSTM的梯度主要通过细胞状态 \(C_t\) 传播，而细胞状态的更新是线性的，梯度路径更加稳定
- 线性关系避免了梯度在时间步之间的连乘，从而缓解了梯度消失问题
灵活的记忆控制：LSTM通过遗忘门和输入门灵活地控制信息的传递，使得模型能够记住有用的信息，并丢弃不必要的信息。

3.5.2 LSTM的缺点¶

计算开销较大，由于包含多个门的计算，训练和推理时需要更多的计算资源
相对于简单的RNN和GRU（门控递归单元），LSTM较为复杂，调参时需要更多的时间和精力

3.6 小结¶

LSTM（Long Short-Term Memory）也称长短时记忆结构, 它是传统RNN的变体, 与经典RNN相比能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时LSTM的结构更复杂, 它的核心结构可以分为四个部分去解析:
- 遗忘门
- 输入门
- 输出门
- 细胞状态
遗忘门结构分析:
- 与传统RNN的内部结构计算非常相似, 首先将当前时间步输入x(t)与上一个时间步隐含状态h(t-1)拼接, 得到[x(t), h(t-1)], 然后通过一个全连接层做变换, 最后通过sigmoid函数进行激活得到f(t), 我们可以将f(t)看作是门值, 好比一扇门开合的大小程度, 门值都将作用在通过该扇门的张量, 遗忘门门值将作用的上一层的细胞状态上, 代表遗忘过去的多少信息, 又因为遗忘门门值是由x(t), h(t-1)计算得来的, 因此整个公式意味着根据当前时间步输入和上一个时间步隐含状态h(t-1)来决定遗忘多少上一层的细胞状态所携带的过往信息.
输入门结构分析:
- 我们看到输入门的计算公式有两个, 第一个就是产生输入门门值的公式, 它和遗忘门公式几乎相同, 区别只是在于它们之后要作用的目标上. 这个公式意味着输入信息有多少需要进行过滤. 输入门的第二个公式是与传统RNN的内部结构计算相同. 对于LSTM来讲, 它得到的是当前的细胞状态, 而不是像经典RNN一样得到的是隐含状态.
细胞状态更新分析:
- 细胞更新的结构与计算公式非常容易理解, 这里没有全连接层, 只是将刚刚得到的遗忘门门值与上一个时间步得到的C(t-1)相乘, 再加上输入门门值与当前时间步得到的未更新C(t)相乘的结果. 最终得到更新后的C(t)作为下一个时间步输入的一部分. 整个细胞状态更新过程就是对遗忘门和输入门的应用.
输出门结构分析:
- 输出门部分的公式也是两个, 第一个即是计算输出门的门值, 它和遗忘门，输入门计算方式相同. 第二个即是使用这个门值产生隐含状态h(t), 他将作用在更新后的细胞状态C(t)上, 并做tanh激活, 最终得到h(t)作为下一时间步输入的一部分. 整个输出门的过程, 就是为了产生隐含状态h(t).
什么是Bi-LSTM?
- Bi-LSTM即双向LSTM, 它没有改变LSTM本身任何的内部结构, 只是将LSTM应用两次且方向不同, 再将两次得到的LSTM结果进行拼接作为最终输出.
LSTM优势:
- LSTM的门结构能够有效减缓长序列问题中可能出现的梯度消失或爆炸, 虽然并不能杜绝这种现象, 但在更长的序列问题上表现优于传统RNN.
LSTM缺点:
- 由于内部结构相对较复杂, 因此训练效率在同等算力下较传统RNN低很多.