2 传统RNN模型¶
学习目标¶
- 了解传统RNN的内部结构及计算公式
- 掌握Pytorch中传统RNN工具的使用
- 了解传统RNN的优势与缺点
适用场景:
- 短序列任务:对于较短的序列,传统RNN仍然是一个可行的选择,例如:简单的文本分类、情感分析等。
- 计算资源有限的场景:在计算资源有限的情况下,传统RNN可以作为一种替代方案。
- 作为学习RNN的基础:学习传统RNN是理解更复杂的RNN变体(如LSTM和GRU)的基础。
不适用场景:
- 长序列任务:对于长序列数据,如长文本、长语音等,传统RNN的表现往往不佳,需要使用LSTM或GRU等更高级的模型。
- 需要长期依赖的任务:对于需要记住长期信息的任务,传统RNN难以胜任。
- 对训练稳定性要求较高的任务:由于梯度问题,传统RNN的训练可能不太稳定,需要仔细调整超参数。
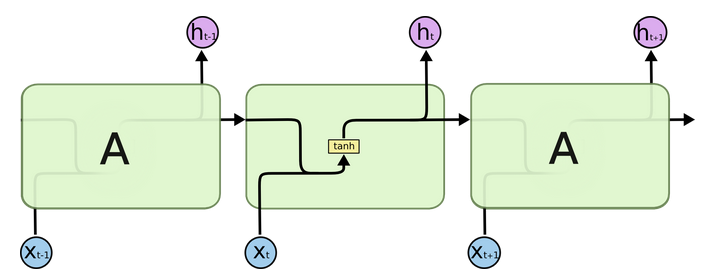
2.1 传统RNN的内部结构图¶
-
结构解释图:

-
内部结构分析:
我们把目光集中在中间的方块部分,它的输入有两部分:分别是\(h_{t-1}\)以及\(x_t\),代表上一时间步的隐藏层输出以及此时间步的输入。它们进入RNN结构体后,会”融合”到一起,这种融合我们根据结构解释可知是将二者进行拼接,形成新的张量[\(x_t\), \(h_{t-1}\)]。之后这个新的张量将通过一个全连接层(线性层),该层使用tanh作为激活函数,最终得到该时间步的输出\(h_t\),它将作为下一个时间步的输入和\(x_{t+1}\)一起进入结构体。以此类推…
-
内部结构过程演示:
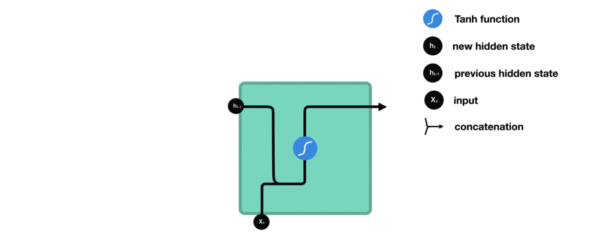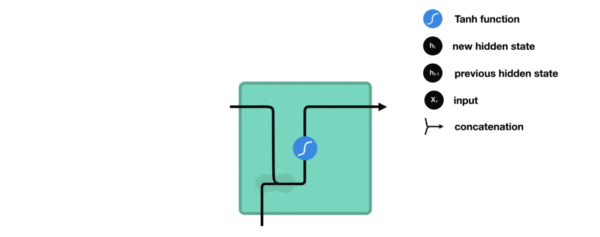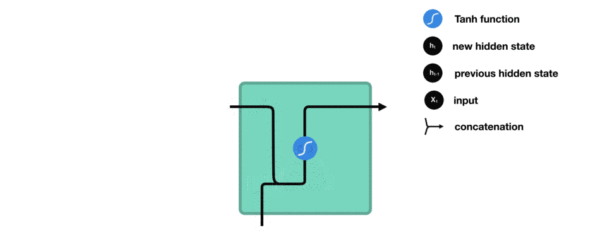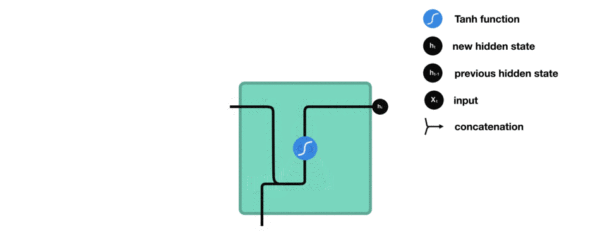
-
根据结构分析得出内部计算公式:
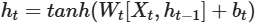
-
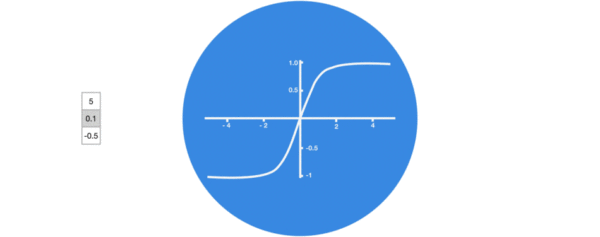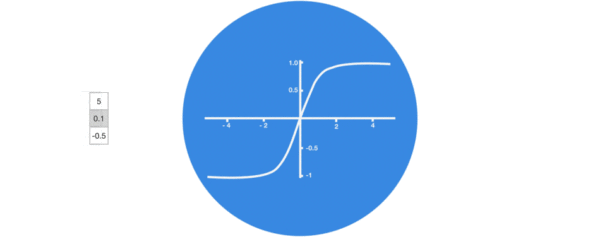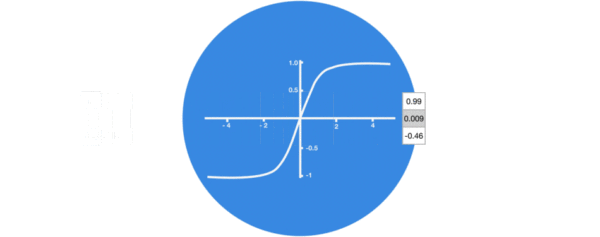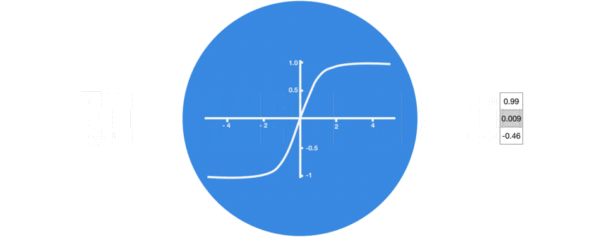
激活函数tanh的作用:用于帮助调节流经网络的值,tanh函数将值压缩在-1和1之间。
2.2 Pytorch构建RNN模型¶
2.2.1 RNN函数¶
Pytorch中RNN函数为:
每个参数的含义如下:
input_size:输入数据的维数,也就是词嵌入的维度hidden_size:隐藏层的维数num_layers:隐藏层的层数batch_first:当batch_first设置为True时,输入的参数x顺序变为:(batch_size, seq_len, input_size)
2.2.2 输入的表示¶
输入的表示形式,输入如下图所示:
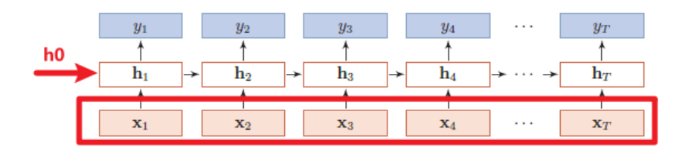
输入主要有向量\(x\)、初始的\(h_0\),其中x:(seq_len, batch_size, input_size),h0:(num_layers, batch, hidden_size),每个参数的含义如下:
seq_len:输入序列的长度, 也就是句子的长度batch_size:批次大小, 句子数input_size:输入特征维度, 就是torch.nn.RNN(input_size,hidden_size,num_layers)中的input_size,二者要保持一致num_layers:隐藏层层数, 与torch.nn.RNN中一致hidden_size:隐藏层维度数, 与torch.nn.RNN中一致
2.2.3 输出的表示¶
RNN的输出可以是\(y\)向量和最后一个时刻隐藏层的输出\(h_T\)
-
输出是\(y\)向量,如下图所示:
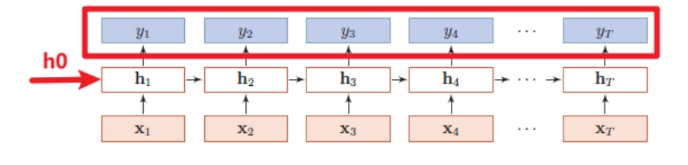
\(y\)向量的结构为out:(seq_len, batch_size, hidden_size),每个参数的意义与上述一致。
-
输出是最后一个时刻隐含层的输出\(h_T\),如下图所示:
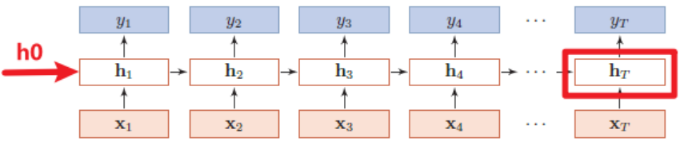
那么ht:(num_layers, batch_size, hidden_size),与h0结构完全一样。
2.2.4 RNN模型构建¶
1.句子长度为1的基础RNN模型代码:
import torch
import torch.nn as nn
def dm_rnn_for_base():
# 第一个参数:input_size(输入张量x的维度)
# 第二个参数:hidden_size(隐藏层的维度,隐藏层的神经元个数)
# 第三个参数:num_layer(隐藏层的数量)
rnn = nn.RNN(input_size=5, hidden_size=6, num_layers=1) # A
# 第一个参数:sequence_length(输入序列的长度),每个句子1个词
# 第二个参数:batch_size(批次的样本数量),3个句子
# 第三个参数:input_size(输入张量的维度),每个词用5维张量表示
input = torch.randn(1, 3, 5) # B
# 第一个参数:num_layer * num_directions(层数*网络方向)
# 第二个参数:batch_size(批次的样本数)
# 第三个参数:hidden_size(隐藏层的维度,隐藏层神经元的个数)
h0 = torch.randn(1, 3, 6) # C
# [1,3,5],[1,3,6] ---> [1,3,6],[1,3,6]
output, hn = rnn(input, h0)
print('output--->',output.shape, output)
print('hn--->',hn.shape, hn)
print('rnn模型--->', rnn)
# 结论: 若句子只有1个词,output输出结果等于hn
输出结果:
output---> torch.Size([1, 3, 6]) tensor([[[ 0.8947, -0.6040, 0.9878, -0.1070, -0.7071, -0.1434],
[ 0.0955, -0.8216, 0.9475, -0.7593, -0.8068, -0.5549],
[-0.1524, 0.7519, -0.1985, 0.0937, 0.2009, -0.0244]]],
grad_fn=<StackBackward0>)
hn---> torch.Size([1, 3, 6]) tensor([[[ 0.8947, -0.6040, 0.9878, -0.1070, -0.7071, -0.1434],
[ 0.0955, -0.8216, 0.9475, -0.7593, -0.8068, -0.5549],
[-0.1524, 0.7519, -0.1985, 0.0937, 0.2009, -0.0244]]],
grad_fn=<StackBackward0>)
rnn模型---> RNN(5, 6)
2.句子长度大于1的RNN模型代码示例:
# 输入数据长度发生变化
def dm_rnn_for_sequencelen():
# 第一个参数:input_size(输入张量x的维度)
# 第二个参数:hidden_size(隐藏层的维度,隐藏层的神经元个数)
# 第三个参数:num_layer(隐藏层的数量)
rnn = nn.RNN(5, 6, 1) # A
# 第一个参数:sequence_length(输入序列的长度),每个句子20个词
# 第二个参数:batch_size(批次的样本数量),3个句子
# 第三个参数:input_size(输入张量的维度),每个词用5维张量表示
input = torch.randn(20, 3, 5) # B
# 第一个参数:num_layer * num_directions(层数*网络方向)
# 第二个参数:batch_size(批次的样本数)
# 第三个参数:hidden_size(隐藏层的维度,隐藏层神经元的个数)
h0 = torch.randn(1, 3, 6) # C
# [20,3,5],[1,3,6] --->[20,3,6],[1,3,6]
output, hn = rnn(input, h0)
print('output--->', output.shape, output)
print('hn--->', hn.shape, hn)
print('rnn模型--->', rnn)
# 结果: 若句子由多个词组成, output的最后一组词向量(每个句子的最后一个词组成)等于h0
输出结果:
output---> torch.Size([20, 3, 6]) tensor([[[-0.1175, 0.9412, 0.4137, 0.8700, -0.9546, -0.8624],
[-0.3786, 0.7321, 0.3956, -0.0332, -0.1671, 0.5342],
[-0.9199, -0.0294, 0.1968, -0.2076, 0.8274, -0.9380]],
...
[[ 0.6937, 0.9086, -0.5759, 0.6497, -0.1622, 0.3149],
[ 0.3938, -0.1056, -0.4888, -0.0488, 0.1909, 0.1397],
[ 0.3134, -0.0552, -0.2793, -0.6143, 0.7715, -0.3820]]],
grad_fn=<StackBackward0>)
hn---> torch.Size([1, 3, 6]) tensor([[[ 0.6937, 0.9086, -0.5759, 0.6497, -0.1622, 0.3149],
[ 0.3938, -0.1056, -0.4888, -0.0488, 0.1909, 0.1397],
[ 0.3134, -0.0552, -0.2793, -0.6143, 0.7715, -0.3820]]],
grad_fn=<StackBackward0>)
rnn模型---> RNN(5, 6)
3.隐藏层大于1的RNN模型代码示例:
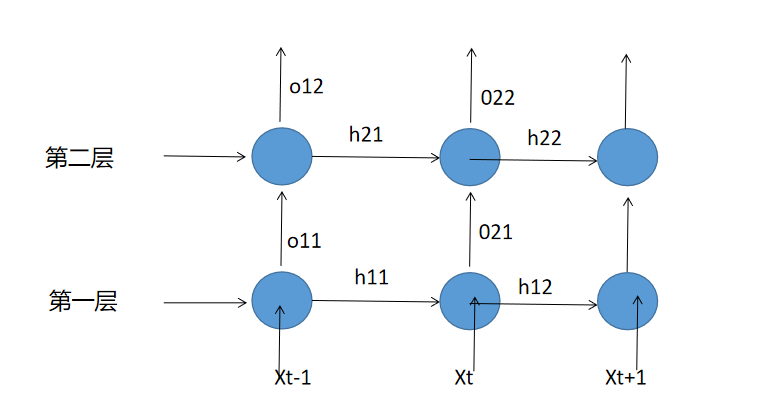
def dm_run_for_hiddennum():
# 第一个参数:input_size(输入张量x的维度)
# 第二个参数:hidden_size(隐藏层的维度, 隐藏层的神经元个数)
# 第三个参数:num_layer(隐藏层的数量)
rnn = nn.RNN(5, 6, 2) # A 隐藏层个数从1-->2 下面程序需要修改的地方?
# 第一个参数:sequence_length(输入序列的长度)
# 第二个参数:batch_size(批次的样本数量)
# 第三个参数:input_size(输入张量的维度)
input = torch.randn(1, 3, 5) # B
# 第一个参数:num_layer * num_directions(层数*网络方向)
# 第二个参数:batch_size(批次的样本数)
# 第三个参数:hidden_size(隐藏层的维度,隐藏层神经元的个数)
h0 = torch.randn(2, 3, 6) # C
output, hn = rnn(input, h0)
print('output-->', output.shape, output)
print('hn-->', hn.shape, hn)
print('rnn模型--->', rnn) # nn模型---> RNN(5, 6, num_layers=2)
# 结论:若只有1个隐藏层,output输出结果等于hn
# 结论:如果有2个隐藏层,hn有2个,output输出结果等于最后1个隐藏层的hn
输出结果:
output--> torch.Size([1, 3, 6]) tensor([[[ 0.4987, -0.5756, 0.1934, 0.7284, 0.4478, -0.1244],
[ 0.6753, 0.5011, -0.7141, 0.4480, 0.7186, 0.5437],
[ 0.6260, 0.7600, -0.7384, -0.5080, 0.9054, 0.6011]]],
grad_fn=<StackBackward0>)
hn--> torch.Size([2, 3, 6]) tensor([[[ 0.4862, 0.6872, -0.0437, -0.7826, -0.7136, -0.5715],
[ 0.8942, 0.4524, -0.1695, -0.5536, -0.4367, -0.3353],
[ 0.5592, 0.0444, -0.8384, -0.5193, 0.7049, -0.0453]],
[[ 0.4987, -0.5756, 0.1934, 0.7284, 0.4478, -0.1244],
[ 0.6753, 0.5011, -0.7141, 0.4480, 0.7186, 0.5437],
[ 0.6260, 0.7600, -0.7384, -0.5080, 0.9054, 0.6011]]],
grad_fn=<StackBackward0>)
rnn模型---> RNN(5, 6, num_layers=2)
2.3 传统RNN优缺点¶
2.3.1 传统RNN的优点¶
由于内部结构简单,对计算资源要求低,相比之后我们要学习的RNN变体(LSTM和GRU模型)参数总量少了很多,在短序列任务上性能和效果都表现优异。
- 结构简单,易于理解和实现:
- 传统RNN的结构非常直观,只有一个隐藏层和循环连接,因此容易理解其工作原理。
- 由于结构简单,其代码实现也相对容易。
- 适用于处理序列数据:
- 传统RNN的核心优势在于它能够处理具有顺序关系的数据,例如文本、语音、时间序列等。
- 通过循环连接,RNN可以将过去的信息传递到当前时刻,从而学习序列数据中的依赖关系。
- 能够处理可变长度的序列:
- 传统RNN可以处理长度不固定的序列,而无需提前固定输入数据的长度。
- 这使得它在处理自然语言、语音等具有可变长度数据的任务中非常灵活。
- 参数共享:
- 传统RNN在每个时间步都共享相同的参数(权重矩阵和偏置项),从而减少了模型参数的数量。
- 参数共享还允许RNN学习序列数据中跨时间步的通用模式。
- 计算效率较高 (相对于更复杂的RNN变体):
- 由于结构简单,传统 NN的计算复杂度相对较低,训练速度相对较快。
- 在一些计算资源有限的场景下,传统RNN是一个可行的选择。
2.3.2 传统RNN的缺点¶
传统RNN在解决长序列之间的关联时,通过实践证明经典RNN表现很差。原因是在进行反向传播的时候,过长的序列导致梯度的计算异常,发生梯度消失或爆炸。
- 梯度消失问题:
- 这是传统RNN最主要的缺点。在处理长序列时,梯度在反向传播过程中会逐渐衰减,导致网络无法学习到长距离依赖关系。
- 梯度消失使得模型难以捕捉输入序列中较早的信息,从而限制了其在长序列任务上的性能。
- 梯度爆炸问题:
- 与梯度消失相反,在某些情况下,梯度在反向传播过程中可能会呈指数级增长,导致训练不稳定甚至发散。
- 梯度爆炸也限制了传统RNN在某些任务中的应用。
- 难以捕捉长期依赖:
- 由于梯度消失问题,传统RNN很难学习长距离的依赖关系,即难以记住输入序列中较早的信息,并将其用于影响后面的输出。
- 这意味着在处理文本、语音等长序列时,传统RNN很难理解上下文的含义。
-
训练不稳定:
- 由于梯度消失和梯度爆炸问题,传统RNN的训练过程可能会不稳定,需要小心调整超参数。
-
无法并行计算:
-
由于RNN的循环结构,每个时间步的计算都依赖于前一个时间步的隐藏状态,因此无法进行并行计算,训练速度受到限制。
-
梯度消失或爆炸介绍
-
根据反向传播算法和链式法则, 梯度的计算可以简化为以下公式:
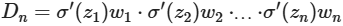
-
其中sigmoid的导数值域是固定的,在[0,0.25]之间。而一旦公式中的w也小于1,那么通过这样的公式连乘后,最终的梯度就会变得非常非常小,这种现象称作梯度消失。反之,如果我们人为的增大w的值,使其大于1,那么连乘够就可能造成梯度过大,称作梯度爆炸。
-
梯度消失或爆炸的危害:
如果在训练过程中发生了梯度消失,权重无法被更新,最终导致训练失败;梯度爆炸所带来的梯度过大,大幅度更新网络参数,在极端情况下,结果会溢出(NaN值)。
-
2.4 小结¶
- 学传统RNN的结构:
- 它的输入有两部分, 分别是h(t-1)以及x(t), 代表上一时间步的隐层输出, 以及此时间步的输入, 它们进入RNN结构体后, 会”融合”到一起, 这种融合我们根据结构解释可知, 是将二者进行拼接, 形成新的张量[x(t), h(t-1)], 之后这个新的张量将通过一个全连接层(线性层), 该层使用tanh作为激活函数, 最终得到该时间步的输出h(t), 它将作为下一个时间步的输入和x(t+1)一起进入结构体. 以此类推.
- nn.RNN类初始化主要参数解释:
- input_size: 输入张量x中特征维度的大小
- hidden_size: 隐层张量h中特征维度的大小
- num_layers: 隐含层的数量
- nonlinearity: 激活函数的选择, 默认是tanh
- nn.RNN类实例化对象主要参数解释:
- input: 输入张量x
- h0: 初始化的隐层张量h
- 传统RNN的优势:
- 由于内部结构简单, 对计算资源要求低, 相比之后我们要学习的RNN变体:LSTM和GRU模型参数总量少了很多, 在短序列任务上性能和效果都表现优异.
- 传统RNN的缺点:
- 传统RNN在解决长序列之间的关联时, 通过实践,证明经典RNN表现很差, 原因是在进行反向传播的时候, 过长的序列导致梯度的计算异常, 发生梯度消失或爆炸.
- 什么是梯度消失或爆炸:
- 根据反向传播算法和链式法则, 得到梯度的计算的简化公式:其中sigmoid的导数值域是固定的, 在[0, 0.25]之间, 而一旦公式中的w也小于1, 那么通过这样的公式连乘后, 最终的梯度就会变得非常非常小, 这种现象称作梯度消失. 反之, 如果我们人为的增大w的值, 使其大于1, 那么连乘够就可能造成梯度过大, 称作梯度爆炸.
- 梯度消失或爆炸的危害:
- 如果在训练过程中发生了梯度消失,权重无法被更新,最终导致训练失败; 梯度爆炸所带来的梯度过大,大幅度更新网络参数,在极端情况下,结果会溢出(NaN值).