4 GRU模型¶

学习目标¶

了解GRU内部结构及计算公式
掌握Pytorch中GRU工具的使用
了解GRU的优势与缺点

4.1 GRU介绍¶

GRU（Gated Recurrent Unit）也称为门控循环单元，是一种改进版的RNN。同LSTM一样能够有效捕捉长序列之间的语义关联，通过引入两个”门”机制（重置门和更新门）来控制信息的流动，从而避免了传统RNN中的梯度消失问题，并减少了LSTM模型中的复杂性。

通过引入更新门 (Update Gate) 和重置门 (Reset Gate) 来控制信息在网络中的流动。这些门控机制决定哪些信息应该保留、哪些信息应该丢弃，从而有效地捕获长距离的依赖关系。

4.1.1 内部结构¶

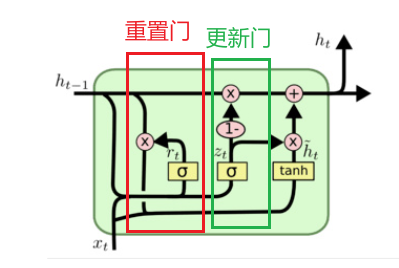
1749049183155

隐藏状态：包含了过去时间步的记忆，并随着时间步的推移不断更新。

重置门：决定在计算候选隐藏状态时，要忽略多少先前的隐藏状态。

更新门：决定在多大程度上保留先前的隐藏状态，以及在多大程度上更新为新的隐藏状态。

候选隐藏状态：基于当前输入和经过重置门过滤后的前一时刻隐藏状态计算出的新的隐藏状态的候选值。

更新后的隐藏状态：最终的隐藏状态，由先前的隐藏状态和候选隐藏状态加权求和得到。

① 重置门（Reset Gate）

决定如何将新的输入与之前的隐藏状态结合。

当重置门值接近0时，表示当前时刻的输入几乎不依赖上一时刻的隐藏状态。
当重置门值接近1时，表示当前时刻的输入几乎完全依赖上一时刻的隐藏状态。

公式：

\(r_t=σ(W_r⋅[h_{t−1},x_t]+b_r)\)

\(r_t\)：重置门的输出
\(W_r\) 和 \(b_r\)：重置门的权重和偏置
\(σ\)：\(sigmoid\)函数，输出值在 0 到 1 之间

② 更新门（Update Gate）

决定多少之前的信息需要保留，多少新的信息需要更新。

当更新门值接近0时，意味着网络只记住旧的隐藏状态，几乎没有新的信息。
当更新门值接近1时，意味着网络更倾向于使用新的隐藏状态，记住当前输入的信息。

公式：

\(z_t=σ(W_z⋅[h_{t−1},x_t]+b_z)\)

\(z_t\)：更新门的输出
\(W_z\) 和 \(b_z\)：更新门的权重和偏置
\(σ\)：\(sigmoid\)函数，输出值在 0 到 1 之间

③ 候选隐藏状态（Candidate Hidden State）

捕捉当前时间步的信息，多少前一隐藏状态的信息被保留。

公式：

\(\tilde{h}_t=tanh⁡(W_h⋅[r_t⊙h_{t−1},x_t]+b_h)\)

\(\tilde{h}_t\)：候选隐藏状态
\(W_h\) 和 \(b_h\)：候选隐藏状态的权重和偏置
\(tanh\)⁡：双曲正切函数，用于将值压缩到 -1 到 1 之间
⊙：逐元素乘法

④ 最终隐藏状态（Final Hidden State）

控制信息更新，传递长期依赖。

公式：

\(h_t=(1−z_t)⊙h_{t−1}+z_t⊙\tilde{h}_t\)

\(h_t\)：当前时间步的隐藏状态
\(z_t\)：更新门的输出，控制新旧信息的比例
⊙：逐元素乘法

4.2 GRU的结构图¶

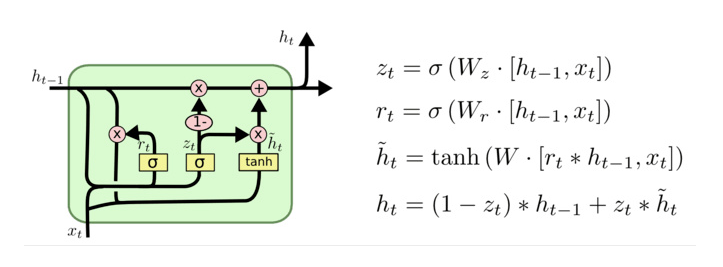
结构解释图:

4.2.1 内部结构分析¶

GRU的更新门和重置门结构图:

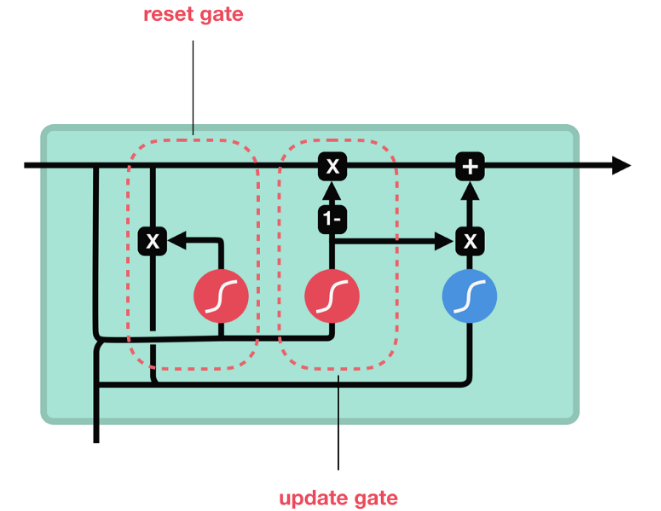
和之前分析过的LSTM中的门控一样:

1.首先计算更新门和重置门的门值，分别是\(z_t\)和\(r_t\)，计算方法就是使用\(x_t\)与\(h_{t-1}\)拼接进行线性变换，再经过\(sigmoid\)激活。

2.之后重置门门值作用在了\(h_{t-1}\)上，代表控制上一时间步传来的信息有多少可以被利用。

3.接着就是使用这个重置后的\(h_{t-1}\)进行基本的RNN计算，即与\(x_t\)拼接进行线性变化，经过\(tanh\)激活，得到新的\(h_t\)。

4.最后更新门的门值会作用在新的\(h_t\)，而1-门值会作用在\(h_{t-1}\)上，随后将两者的结果相加，得到最终的隐藏状态输出\(h_t\)。

5.这个过程意味着更新门有能力保留之前的结果，当门值趋于1时，输出就是新的\(h_t\)；而当门值趋于0时，输出就是上一时间步的\(h_{t-1}\)。

4.2.2 GRU工作流程：¶

计算重置门 \(r_t\) 和更新门 \(z_t\)。
根据重置门的结果计算候选隐藏状态 \(\tilde{h}_t\)。
使用更新门将候选隐藏状态与上一时刻的隐藏状态结合，得到当前时刻的隐藏状态 \(h_t\)。
将 \(h_t\) 作为输出，并传递到下一时刻。

4.3 Bi-GRU介绍¶

Bi-GRU（Bidirectional Gated Recurrent Unit）是 GRU的改进，它通过将正向和反向GRU结合在一起，能够同时利用输入序列的过去和未来信息。双向GRU是一种在序列建模中常见的结构，尤其在自然语言处理（NLP）和时间序列分析中具有很大的优势。

它的核心思想同时利用序列的正向和反向信息：

正向 GRU：从序列的起始位置到结束位置处理数据，捕捉过去的信息。
反向 GRU：从序列的结束位置到起始位置处理数据，捕捉未来的信息。

将正向和反向GRU的隐藏状态结合起来，得到更全面的序列表示。

4.3.1 内部结构¶

输入层：将输入序列传递给两个GRU网络（正向和反向）。

正向GRU：按照时间顺序处理输入序列（从第一个时间步到最后一个时间步）。

反向GRU：逆序处理输入序列（从最后一个时间步到第一个时间步）。

合并层：正向和反向GRU的输出通常被拼接在一起，形成一个包含更多上下文信息的表示。

输出层：将合并后的表示传递到下游任务，进行分类、回归或者其他任务的预测。

① 正向 GRU

输入：序列的正向数据 \(x_1,x_2,…,x_T\)。
隐藏状态：\(\overrightarrow{h_t}\)。

② 反向 GRU

输入：序列的反向数据 \(x_T,x_{T−1},…,x_1\)。
隐藏状态：\(\overleftarrow{h_t}\)。

③ 结合正向和反向信息

将正向和反向的隐藏状态拼接起来，生成最终的隐藏状态：

\(h_t=[\overrightarrow{h_t},\overleftarrow{h_t}]\)
最终的隐藏状态 \(ht\) 包含了序列的完整上下文信息。
,：表示拼接操作。

④ 输出层：

将双向隐藏状态输入到输出层，得到最终的输出 \(y_1, y_2, ..., y_T\)。
输出层可以是线性层、softmax层等，根据具体任务而定。

4.3.2 Bi-GRU的优缺点¶

Bi-GRU的优点
- 捕捉上下文信息：通过结合正向和反向的信息，Bi-GRU能够更好地捕捉序列的上下文依赖关系
- 适用于需要全局信息的任务：在自然语言处理（NLP）等任务中，Bi-GRU能够同时考虑过去和未来的信息
- 性能优于单向GRU：在许多任务中，Bi-GRU的表现优于单向GRU
Bi-GRU的缺点
- 计算复杂度高：Bi-GRU需要同时计算正向和反向的GRU，计算量是单向GRU的两倍
- 参数量大：Bi-GRU的参数比单向GRU多，训练时间较长
- 难以并行化：与GRU类似，Bi-GRU需要按时间步依次计算

4.4 Pytorch构建GRU模型¶

4.4.1 GRU函数¶

PyTorch通过torch.nn.GRU类提供GRU实现：

Python

gru = nn.GRU(input_size, hidden_size, num_layers, bidirectional, batch_first, dropout)

具体参数说明如下：

input_size：输入特征的维度
hidden_size：隐藏层的维度
num_layers：GRU的层数（默认值为1）
batch_first：如果为True，输入和输出的形状为 (batch_size, seq_len, input_size)；否则为 (seq_len, batch_size, input_size)
bidirectional：如果为True，使用双向GRU；否则为单向GRU（默认False）
dropout：在多层GRU中，是否在层之间应用dropout（默认值为0）

GRU的输入表示为：

输入数据x: (seq_len, batch_size, input_size)
初始隐藏状态h_0: (num_layers * num_directions, batch_size, hidden_size)

GRU的输出是一个元组(output, h_n):

output:包含最后一层在所有时间步的隐藏状态
- 单向: (seq_len, batch_size, hidden_size)
- 双向: (seq_len, batch_size, hidden_size * 2)
h_n (最终隐藏状态):所有层的最后一个时间步的隐藏状态
- 单向: (num_layers, batch_size, hidden_size)
- 双向: (num_layers * 2, batch_size, hidden_size)

4.4.2 GRU实践¶

Python

# 定义GRU的参数含义: (input_size, hidden_size, num_layers)
# 定义输入张量的参数含义: (sequence_length, batch_size, input_size)
# 定义隐藏层初始张量的参数含义: (num_layers * num_directions, batch_size, hidden_size)
import torch.nn as nn
import torch


def dm_gru():
    # 创建GRU层
    gru = nn.GRU(input_size=5, hidden_size=6, num_layers=2)
    # 创建输入张量
    input = torch.randn(size=(1, 3, 5))
    # 初始化隐藏状态
    h0 = torch.randn(size=(2, 3, 6))
        # hn输出两层隐藏状态, 最后1个隐藏状态值等于output输出值
    output, hn = gru(input, h0)
    print('output--->', output.shape, output)
    print('hn--->', hn.shape, hn)

输出结果:

Python

output---> torch.Size([1, 3, 6]) tensor([[[-0.1109, -1.0413,    0.3340,    0.6548, -0.1967,    0.4516],
                 [ 0.0095,    1.0576, -0.3029,    0.2907, -0.3876,    0.4790],
                 [ 0.3430, -1.2316,    0.5145,    1.0067,    0.2637,    0.1618]]],
             grad_fn=<StackBackward0>)
hn---> torch.Size([2, 3, 6]) tensor([[[ 0.1325,    0.5354,    0.3423, -0.6943,    0.9261, -0.0672],
                 [ 0.6470,    0.3491, -0.3319, -0.8313,    0.0370, -0.2859],
                 [ 0.2856, -0.7553,    1.2566, -0.0828,    0.4304, -0.1633]],

                [[-0.1109, -1.0413,    0.3340,    0.6548, -0.1967,    0.4516],
                 [ 0.0095,    1.0576, -0.3029,    0.2907, -0.3876,    0.4790],
                 [ 0.3430, -1.2316,    0.5145,    1.0067,    0.2637,    0.1618]]],
             grad_fn=<StackBackward0>)

4.5 GRU的优缺点¶

4.5.1 GRU的优点¶

比LSTM更简单：GRU只有两个门（与LSTM的三个门相比），因此它的计算复杂度更低，训练和推理速度较快。
避免梯度消失：通过更新门和重置门的设计，GRU可以有效地捕获长时依赖。
- 更新门值≈0时，\(ht≈h_{t−1}\)，梯度通过 \(h_{t−1}\) 直接传递，形成残差连接（类似 ResNet），避免梯度消失。
- 更新门值≈1时，\(ht≈\tilde{h}_t\)，梯度通过非线性变换传播，但门控的平滑性可抑制梯度爆炸。
- 重置门值≈0时，\(h_{t−1}\) 对候选状态的贡献被抑制，模型更依赖当前输入 \(x_t\)。
- 重置门值≈1时，\(h_{t−1}\) 完全参与候选状态计算，保留长期依赖。
- 线性路径：更新门的残差连接 (\(h_t=(1−z_t)⊙h_{t−1}+z_t⊙\tilde{h}_t\)) 允许梯度在时间步间直接传递，减少连乘效应。
- 门控的平滑性：Sigmoid 函数输出值在 [0, 1] 之间，避免梯度剧烈波动。
性能与LSTM相当：在很多任务中，GRU和LSTM的表现非常接近，GRU的性能往往能够与LSTM相匹敌，但需要的计算资源较少。

4.5.2 GRU的缺点¶

对超长序列的捕捉能力弱于LSTM：LSTM 通过独立的细胞状态（Cell State）显式存储长期信息，而 GRU 直接更新隐藏状态，可能导致长程依赖信息逐渐稀释。
门控机制的非线性限制：更新门和重置门的 Sigmoid 激活函数可能导致梯度饱和（接近 0 或 1），影响参数更新。LSTM 的细胞状态更新包含线性操作（\(C_t=f_t⋅C_{t−1}+i_t⋅\tilde{C}_t\)），梯度传播更稳定。
不可并行计算：时间步之间的依赖关系仍然限制了其并行化程度。

4.6 小结¶

GRU（Gated Recurrent Unit）也称门控循环单元结构, 它也是传统RNN的变体, 同LSTM一样能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时它的结构和计算要比LSTM更简单, 它的核心结构可以分为两个部分去解析:
- 更新门
- 重置门
内部结构分析:
- 和之前分析过的LSTM中的门控一样, 首先计算更新门和重置门的门值, 分别是z(t)和r(t), 计算方法就是使用X(t)与h(t-1)拼接进行线性变换, 再经过sigmoid激活. 之后重置门门值作用在了h(t-1)上, 代表控制上一时间步传来的信息有多少可以被利用. 接着就是使用这个重置后的h(t-1)进行基本的RNN计算, 即与x(t)拼接进行线性变化, 经过tanh激活, 得到新的h(t). 最后更新门的门值会作用在新的h(t)，而1-门值会作用在h(t-1)上, 随后将两者的结果相加, 得到最终的隐含状态输出h(t), 这个过程意味着更新门有能力保留之前的结果, 当门值趋于1时, 输出就是新的h(t), 而当门值趋于0时, 输出就是上一时间步的h(t-1).
Bi-GRU与Bi-LSTM的逻辑相同, 都是不改变其内部结构, 而是将模型应用两次且方向不同, 再将两次得到的LSTM结果进行拼接作为最终输出. 具体参见上小节中的Bi-LSTM.
GRU的优势:
- GRU和LSTM作用相同, 在捕捉长序列语义关联时, 能有效抑制梯度消失或爆炸, 效果都优于传统RNN且计算复杂度相比LSTM要小.
GRU的缺点:
- GRU仍然不能完全解决梯度消失问题, 同时其作用RNN的变体, 有着RNN结构本身的一大弊端, 即不可并行计算, 这在数据量和模型体量逐步增大的未来, 是RNN发展的关键瓶颈.